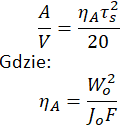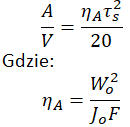Projektowanie Sprężyn
Spis treści
Projektowanie sprężyn o pręcie skręcanym
-
Projektowanie sprężyny o pręcie skręcanym dla obciążeń statycznych
-
Wytrzymałość sprężyny liczona za pomocą współczynnika kształtu i wymiaru przekroju
-
Sprężyny śrubowe walcowe, naciskowe z drutu okrągłego
-
Zestawienie wzorów dla sprężyn o pręcie skręcanym.
Projektowanie sprężyn dla obciążeń dynamicznych
-
Projektowanie sprężyn dla obciążeń dynamicznych
Sprężyny zginane
-
Obliczenia sprężyn o pręcie zginanym
-
Wzory obliczeniowe dla sprężyn zginanych
Projektowanie sprężyn o pręcie skręcanym
Projektowanie sprężyn należy zacząć od określenia charakteru obciążeń na sprężynie. Należy wziąć pod uwagę wykonanie obliczeń dla dwóch przypadków. Pierwszy to przypadek statyczny, w którym obciążenia się nie zmieniają a sprężyna jest stale obciążona niezmienną siłą. Drugi to przypadek dynamiczny, dla którego siła działająca na sprężynę ulega zmianie dynamicznie w czasie.
Klasyczne sprężyny zawinięte, obciążone wzdłuż osi walca, po którym są zawinięte należą do sprężyn o pręcie skręcanym, gdyż mimo tego, że siła ściska sprężynę to poprzez taką geometrię skręca pręt.
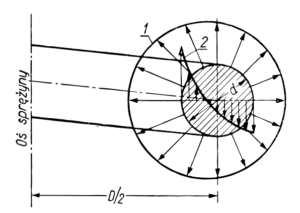
W przypadku skręcania pręta zawiniętego (np. klasyczne sprężyny śrubowe) , rozkład naprężeń ścinających wywołanych momentem skręcającym, poprzez zagięcie pręta nie jest rozmieszczone wokół osi centralnej przekroju pręta sprężyny. Efekt ten uwzględniany jest w obliczeniach poprzez dodanie η_AS – współczynnika równomierności rozmieszczenia naprężeń
Głównym kryterium przy projektowaniu sprężyny o pręcie skręcanym jest wytrzymałość pręta na skręcanie, zatem naprężenia styczne.
Naprężenia styczne muszą być mniejsze niż dopuszczalne naprężenia dla danego materiału.
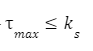
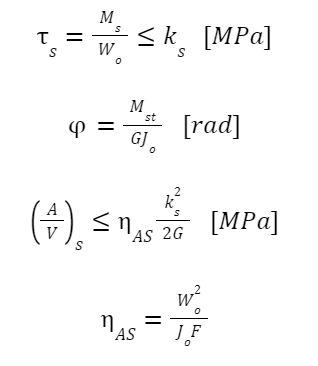
Gdzie:
τ_s – naprężenia styczne wywołane momentem skręcającym. Maksymalne naprężenia styczne to τ_max. Nie mogą one przekraczać k_s – dopuszczalnych naprężeń stycznych w materiale.
W_o – wskaźnik przekroju pręta na skręcanie
M_st/M_s – moment skręcający
η_AS – współczynnik równomierności rozmieszczenia naprężeń w pręcie skręcanym – wywołany zagięicem pręta wokół osi i przesunięciem naprężeń skręcanych w kierunku osi sprężyny czasami oznaczany η_A
k_s – wartośc naprężeń stycznych dopuszczalnych dla mateirału z którego zrobiona jest sprężyna
φ – kąt skręcenia
Projektowanie sprężyny o pręcie skręcanym dla obciążeń statycznych
W pierwszej kolejności, w jaki sposób należy liczyć naszą spręzynę należy wziąć pod uwagę poniższe wzory.
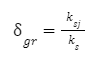 |
Jest to graniczna wartość współczynnika stałości obciążenia, przy której uzyskuje się jednakowe bezpieczeństwo w warunkach statycznych i dynamicznych |
|
Jeśli współczynnik stałości obciążenia wynosi
|
To o wytrzymałości decyduje wytrzymałość statyczna |
|
Jeśli współczynnik stałości obciążenia wynosi
|
To o wytrzymałości decyduje wytrzymałość zmęczeniowa |
Gdzie:
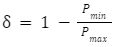 |
– współczynnik stałości obciążeń. |
k_sj – dopuszczalne naprężenia skręcające jednostronnie zmienne.
k_s – dopuszczalne naprężenia skręcające dla obciażeń stałych.
P_min – Siła minimalna o charakterze zmiennym występująca w sprężynie.
P_max – Siła minimalna o charakterze zmiennym występująca w sprężynie.
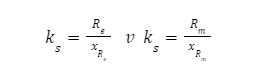
Re – Granica plastyczności w próbce rozciąganej.
Rm – granica wytrzymałości – stosowane dla stali twardych, pękających.
Współczynnik bezpieczeństwa dla Granicy plastyczności i granicy wytrzymałości
Wytrzymałość sprężyny liczona za pomocą wsółczynnika kształtu i wymiaru przekroju:
g_k – współczynnik kształtu
g_w – współczynnik przekroju, zazwyczaj pozyskiwane z gotowych tablic
g_f – współczynnik wytrzymałości przekroju pręta
Tablica wartości powyższych współczynników dla sprężyn o pręcie skręcanym o przekroju okrągłym
| D/d | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 | 16 |
| g_k | 0,645 | 0,725 | 0,775 | 0,813 | 0,833 | 0,855 | 0,870 | 0,884 | 0,905 | 0,918 | 0,925 |
| g_d | 0,292 | 0,268 | 0,248 | 0,232 | 0,2175 | 0,206 | 0,196 | 0,187 | 0,173 | 0,161 | 0,152 |
| g_f | 0,1075 | 0,0905 | 0,0775 | 0,0677 | 0,0595 | 0,0534 | 0,0489 | 0,0446 | 0,0381 | 0,033 | 0,0194 |
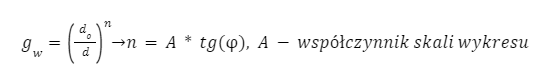
d_o – średnica próbki służącej do wyznaczania cech wytrzymałościowych materiału
Zazwyczaj:
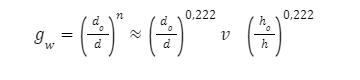
Uwzględniając współczynniki kształtu i wymiaru przekroju naprężenia ścinające:
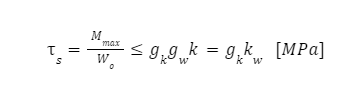
| – dopuszczalne naprężenie dla pręta prostego uwzględniające wymiary przekroju i warunki obciążenia |
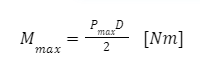
Oraz
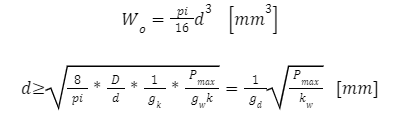
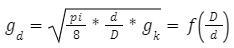 |
– współczynnik wytrzymałościowy średnicy pręta |
Wzór na poel przekroju (a zatem także pośrednio wzór na średnicę pręta) pręta sprężyny wynosi więc :
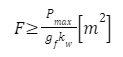
| – współczynnik wytrzymałości przekroju pręta | |
| F | – pole przekroju pręta sprężyny |
Zestawienie wzorów dla sprężyn o pręcie skręcanym
Najważniejsze wzory dla drążka skrętnego.
| Naprężenie w drążku skręcanym | Kąt skręcenia drążka skrętnego | Współczynnik sztywności dla drążka skręcanego | Praca odkształcenia sprężyny | Zdolność akumulowania energii drążka skrętnego |
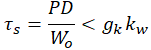 |
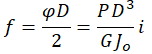 |
|
Najważniejsze wzory dla sprężyny śrubowej o różnych przekrojach.
| Naprężenie w sprężynie śrubowej | Strzałka ugięcia sprężyny śrubowej | Współczynnik sztywności sprężyny śrubowej | Praca odkształcenia sprężyny śrubowej | Zdolność akumulowania energii sprężyny śrubowej |
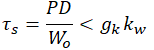 |
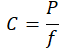 |
 |
|
Dla pręta o przekroju okrągłym.
| Średnica, przekrój pręta | Ugięcie zwoju f/i | Wskaźnik wytrzymałości przekroju w osi przekroju | Moment bezwładności przekroju w osi | Współczynnik równomierności rozmieszczenia naprężeń |
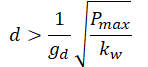 |
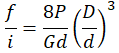 |
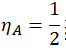 |
Dla pręta o przekroju prostokątnym.
| Średnica, przekrój pręta (g_f i k_w z wzorów powyżej) | Ugięcie zwoju f/i | Wskaźnik wytrzymałości przekroju w osi przekroju | Moment bezwładności przekroju w osi | Współczynnik równomierności rozmieszczenia naprężeń |
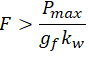 |
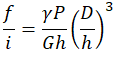 |
Wartości współczynników do obliczania spręzyn śrubowych o prostokątnym pręcie skręcanym
| b/h | 1,0 | 1,5 | 2 | 3 | 4 | 5 |
| η_2 | 0,208 | 0,231 | 0,246 | 0,267 | 0,282 | 0,29 |
| η_3 | 0,140 | 0,196 | 0,229 | 0,263 | 0,281 | 0,29 |
| 0,308 | 0,272 | 0,264 | 0,272 | 0,282 | 0,29 | |
| γ | 5,60 | 2,67 | 1,70 | 1 | 0,7 | 0,54 |
Sprężyny śrubowe walcowe, naciskowe z drutu okrągłego:
Sprężyny śrubowe o niewielkich wymiarach i masie charakteryzują się szeregiem korzystnych właściwości, które sprawiają, że są one efektywnym elementem konstrukcyjnym w różnych zastosowaniach.
Wysoka podatność – dzięki niewielkim wymiarom mogą ulegać odkształceniom, co pozwala na ich elastyczne zastosowanie w mechanizmach.
Zdolność do akumulacji energii – ich budowa umożliwia magazynowanie energii mechanicznej.
Brak dodatkowych uchwytów – pozwala to na oszczędność przestrzeni oraz uproszczenie konstrukcji.
Efektywne wykorzystanie materiału i przestrzeni – kompaktowe wymiary i przemyślana konstrukcja maksymalizują funkcjonalność przy minimalnym zużyciu surowca.
Centryczne przeniesienie siły – konstrukcja śruby umożliwia równomierne rozłożenie obciążeń, co zwiększa jej trwałość i niezawodność.
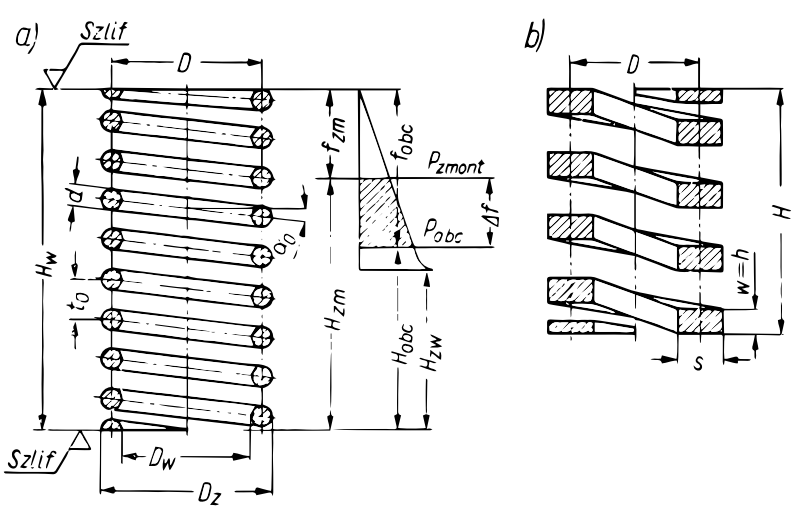
Końce takich śrub są precyzyjnie zaciśnięte oraz szlifowane na co najmniej ¾ obwodu, co zapewnia ich stabilność i dokładność działania. W przypadku sprężyn o dużych średnicach (oznaczanych jako duże d), końcówki są dodatkowo rozkuwane, co wzmacnia ich konstrukcję i poprawia ich parametry użytkowe.
Dla sprężyny w stanie nieobciążonym kąt wznosu linii śrubowej powinien wynosić 8°. Taka wartość zapewnia odpowiednie warunki pracy sprężyny, pozwalając na jej optymalne odkształcenie oraz efektywne gromadzenie i oddawanie energii. Zachowanie tego parametru gwarantuje równowagę pomiędzy wytrzymałością a elastycznością konstrukcji.
Jednym z parametrów obliczeniowych sprężyn jest strzałka ugięcia jednego zwoju
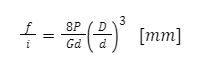
| – całkowita liczba zwojów sprężyny, wartość 1,5…2 wynika z zagięcia i zeszlifowania pierwszego i ostatniego zwoju sprężyny w celu zapewnienia odpowiedniego podparcia | |
Wysokość sprężyny
Sprężyna powinna być zaprojektowana w taki sposób, aby nawet przy największym dopuszczalnym obciążeniu (Qmax) został zachowany minimalny luz między zwojami. Jest to ważne dla zapewnienia trwałości sprężyny oraz jej efektywnej pracy, zapobiegając zjawisku trwałego odkształcenia i nadmiernego zużycia.
Przyjmuje się, że w stanie zwartym w przekroju pręta osiowego wartość naprężenia równa jest granicy sprężystości.
| – wysokość spreżyny zwartej (ściśniętej do punktu zwarcia zwojów) |
| – wysokość sprężyny obciążonej |
Gdzie
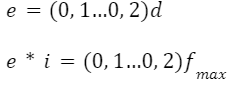
e – najmniejszy luz między zwojami pod obciążeniem P_max
dodatkowo
| – wysokość sprężyny zamontowanej pod obciążeniem P_min | |
| |
– wysokość sprężyny w stanie wolnym – nieobciążonej |
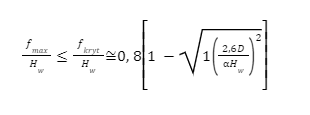
Gdzie:
α – współczynnik zależny od sposobu osadzenia i obciążenia sprężyny
- α≅1 – dla sprężyn bez prowadzenia
- α≅0,5 – dla sprężyn dokładnie prowadzonych
- α≅2 – dla sprężyn dodatkowo zginanych
Wyboczenie sprężyny
Wyboczenie sprężyny to zjawisko polegające na utracie stabilności osiowej sprężyny pod wpływem siły ściskającej, co prowadzi do jej deformacji w kierunku poprzecznym. Wyboczenie jest szczególnie istotnym problemem w sprężynach o dużej smukłości, czyli takich, gdzie stosunek długości sprężyny do średnicy jest wysoki.
Wyboczenie sprężyny możliwe jedynie przy
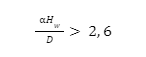
Wybór stosunków obciążeń:

Projektowanie sprężyn dla obciążeń dynamicznych – zmęczeniowych
Dopuszczalne naprężenia ścinające przy obciążeniu jednostronnie zmiennym (tętniącym)
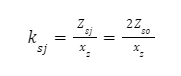
Gdzie:
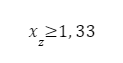
Dla ograniczonej liczby zmian 10^3 < N < 10^6 Zamiast Zso przyjąć odpowiedną wartość z krzywej Wohlera dla próbki skręcanej.
przykładowe orientacyjne wartości parametrów dla Prętów skręcanych
![]()
Parametry wytrzymałościowe dla druta d_o=5mm ze stali węglowej lub stopowej ciągnionego i zwijanego na zimno
| Rodzaj drutu | Z_so | k_s | k_sj | k_sj/k_s |
| Drut ciągniony | 150-170 | 500-550 | 220,5-250,5 | 0,40-0,45 |
| Drut szlifowany | 200-250 | 550-600 | 300-370,5 | 0,55-0,65 |
| Drut szlifowany oraz hartowany i niskoodpuszczany | 280-320 | 600-750 | 420-480 | 0,65-0,75 |
Parametry wytrzymałościowe dla grubego druta zwijanego na gorąco, hartowanego i nisko odpuszczanego
| Rodzaj drutu | Z_so | k_s | k_sj | k_sj/k_s |
| Walcowany | 40-60 | 300-405 | 60-90 | 0,2-0,3 |
| Szlifowany | 100-160 | 400-550 | 150-240 | 0,35-0,45 |
Parametry wytrzymałościowe dla pręta ze stali – sprężynowej chromowo-wanadowej 50HF PN-74/H-84032 hartowany i niskoodpuszczony
| Rodzaj Pręta | Z_so | k_s | k_sj | k_sj/k_s | ||
| Ø20 | Ø40 | Ø60 | ||||
| Pręt szlifowany | 200 | 170 | 100 | 500-650 | 150-300 | 0,3-0,45 |
| Pręt zgniatany | 300 | 280 | 200 | 300-405 | 300-450 | 0,5-0,6 |
Sprężyny zginane
Sprężyny o pręcie zginanym to szczególny rodzaj sprężyn, w których głównym mechanizmem pracy jest odkształcenie sprężyste pręta pod wpływem działania momentu zginającego. Ich konstrukcja i zasada działania różnią się od klasycznych sprężyn opartych na ściskaniu, rozciąganiu lub skręcaniu.
Linie ugięcia sprężyn płaskich, dla różnych wariantów obciążeń
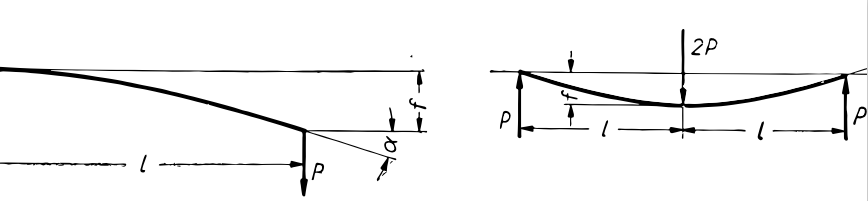
Przyjmuje się , że sprężyna płaska ma małą krzywiznę, tzn. promień gięcia znajduje się w nieskończoności ρ≈∞.
Sprężyny o zmiennym przekroju stosuje się dla zwiększenia podatności. Opisują je modele belki o równej wytrzymałości (naprężenia równe na całej długości).
Przykład prętów o równej wytrzymałości
a) Pręt o stałym przekroju obciążony momentem gnącym. Taki pręt jest równomiernie obciążony na całej długości
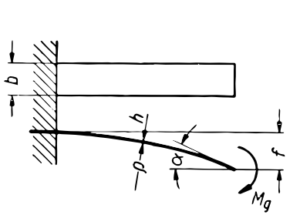
b) Pręt trójkątny obciążony siłą na końcu. Taki pręt również obciążony jest równomiernie na całej długości
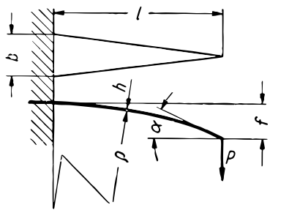
Obliczenia sprężyn o pręcie zginanym
Pręt sprężyny ugina się pod wpływem obciążenia, co powoduje gromadzenie energii potencjalnej w wyniku odkształcenia materiału. Po usunięciu obciążenia sprężyna powraca do pierwotnego kształtu dzięki sprężystości materiału.
Warunki obliczeniowe
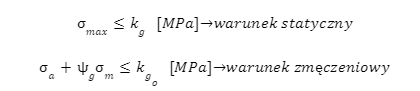
Gdzie:

Wytrzymałość zmęczeniowa dla stali sprężynowej:
Z wykresu Haigha
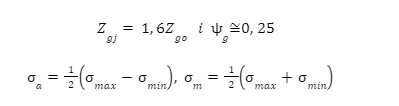
Dodatkowo :
δ-współczynnik stałości obciążenia pręta zginanego

W pierwszej kolejności, w jaki sposób należy liczyć naszą sprężynę, należy wziąć pod uwagę poniższe wzory.
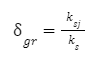 |
Jest to graniczna wartość współczynnika stałości obciążenia, przy której uzyskuje się jednakowe bezpieczeństwo w warunkach statycznych i dynamicznych |
|
Jeśli współczynnik stałości obciążenia wynosi
|
To o wytrzymałości decyduje wytrzymałość statyczna |
|
Jeśli współczynnik stałości obciążenia wynosi
|
To o wytrzymałości decyduje wytrzymałość zmęczeniowa |
Gdzie:
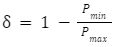 |
– współczynnik stałości obciążeń. |
k_sj – dopuszczalne naprężenia skręcające jednostronnie zmienne.
k_s – dopuszczalne naprężenia skręcające dla obciażeń stałych.
P_min – Siła minimalna o charakterze zmiennym występująca w sprężynie.
P_max – Siła minimalna o charakterze zmiennym występująca w sprężynie.
Naprężenia dopuszczalne skręcające przy obciążeniu statycznym:
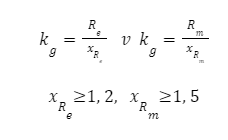
Naprężenia dopuszczalne skręcające dla wytrzymałości zmęczeniowej:
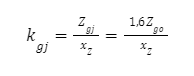
Współczynnik bezpieczeństwa można przyjąć

Przykładowe orientacyjne wartości parametrów wytrzymałościowych dla Prętów zginanych
![]()
Pręt ze stali stopowej hartowanej i nisko odpuszczonej z Re~ 1400MPa
| Rodzaj Pręta | Z_go | k_g | k_gj | k_gj/k_g |
| Pręt walcowany | 130-210 | 550-750 | 160-250 | 0,25-0,35 |
| Pręt kulkowany | 310-340 | 650-900 | 370-400 | 0,45-0,55 |
| Pręt szlifowany | 410-460 | 700-950 | 500-550 | 0,55-0,70 |
Wzory obliczeniowe dla sprężyn zginanych
Wzór wytrzymałościowy, po lewej stronie jednakowy dla warunków statycznych i zmęczeniowych – w przypadku zmęczeniowych podstawiamy wartości momentów zmęczeniowych oraz zmieniamy k – które dla statycznych wynosi k_g ulega zmianie na k_gj :
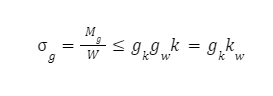
gw – współczynnik wymiarowy, można przyjąć taki sam dla prętów skręcanych
gk – współczynnik kształtu pręta, jedynie uwzględniany w przypadku dużej krzywizny pręta (duży stosunek wymiaru przekroju do promienia krzywizny w płaszczyźnie działania momentu gnącego
k_g – dopuszczalne naprężenia dla materiału w przypadku zginania.
k_gj – dopuszczalne naprężenia dla materiału w przypadku zginania jednostronnego zmiennego.
Współczynniki kształtu dla pręta zginanego sprężyny
| D/d lub Ds. | 3 | 4 | 5 | 6 | 8 | 10 |
| Przekrój okrągły | 1,33 | 1,23 | 1,17 | 1,13 | 1,08 | 1,05 |
| Prostokątny | 1,29 | 1,20 | 1,15 | 1,12 | 1,08 | 1,06 |
Według rodzaju pręta
Dla pręta o stałym przekroju
| Naprężenia od zginania (charakter normalny do powierzchni przekroju) | Strzałka ugięcia | Kąt wychylenia końca pręta | Współczynnik równomierności rozmieszczenia naprężeń |
Dla pręta trapezowego
| Naprężenia od zginania (charakter normalny do powierzchni przekroju) | Strzałka ugięcia | Kąt wychylenia końca pręta | Współczynnik równomierności rozmieszczenia naprężeń |
Współczynniki dla pręta trapezowego
| b_o/L | 1,0 | 0,8 | 0,6 | 0,4 | 0,2 | 0 |
| y1 | 1,0 | 1,05 | 1,12 | 1,20 | 1,31 | 1,5 |
| y2 | 1,0 | 1,07 | 1,17 | 1,30 | 1,49 | 2,0 |
| ηA | 0,111 | 0,130 | 0,155 | 0,19 | 0,242 | 0,333 |
Dla pręta obciążonego momentem gnącym
| Naprężenia od zginania (charakter normalny do powierzchni przekroju) | Strzałka ugięcia | Kąt wychylenia końca pręta | Współczynnik równomierności rozmieszczenia naprężeń |
Gdzie współczynniki rozróżniamy w zalezności od rodzajów pręta
Współczynniki dla pręta prostokątnego
| Wskaźnik wytrzymałości przekroju | Moment bezwładności przekroju | Obiętość czynna pręta sprężyny | Współczynnik równomierności rozmieszczenia naprężeń |
Dla pręta okrągłego
| Wskaźnik wytrzymałości przekroju | Moment bezwładności przekroju | Obiętość czynna pręta sprężyny | Współczynnik równomierności rozmieszczenia naprężeń |