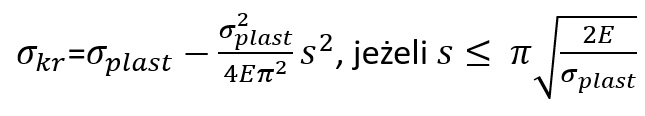Obliczenia belek zginanych, skręcanych i ściskanych, rozkłady naprężeń w belkach, wyboczenie prętów
Spis treści
Schemat belki – obliczenia z objaśnieniami
Układy statycznie niewyznaczalne – równania i przykład
-
Równania równowagi statycznej
-
Brakujące równanie
Wyboczenie prętów – objaśnienie i równania
-
wzór Eulera
-
Krytyczne naprężenie ściskające, które prowadzi do wyboczenia
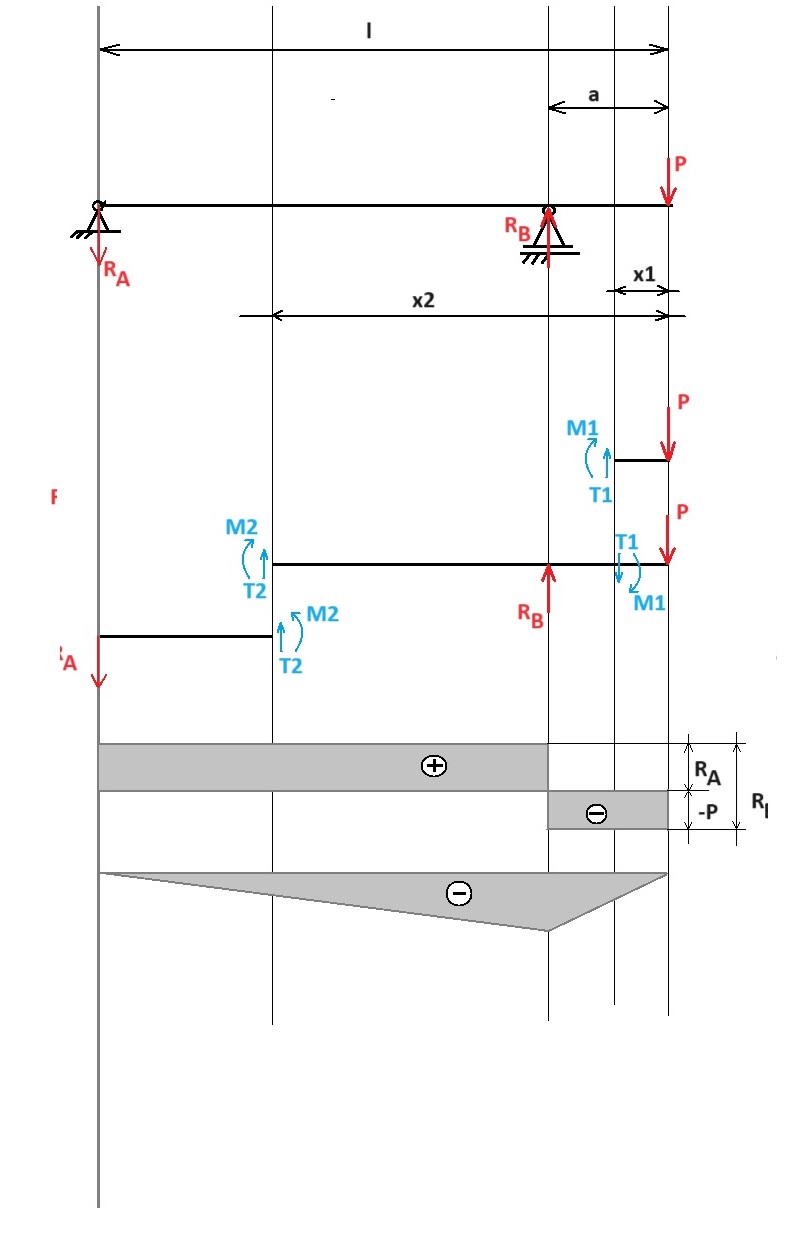
Schemat belki – obliczenia z objaśnieniami
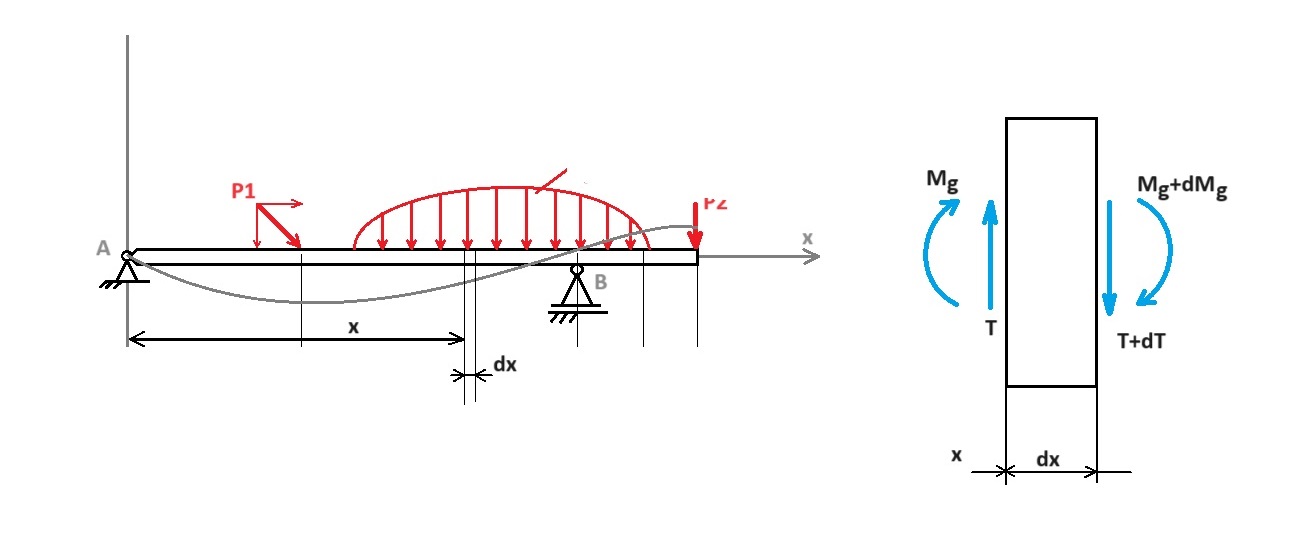
qx – obciążenie ciągłe
Wyznaczamy równania równowagi statycznej.
Aby układ pozostawał w równowadze suma sił w osi y musi być równa 0. Suma sił w osi X musi być równa 0 oraz suma momentów sił działających na układ musi być równa 0.

| – pochodne drugiego rzędu w przypadku zginania belki można pominąć gdyż dążą do 0 |
![]()
Po wyprowadzeniu z powyższych równań sił T, RB oraz RA możemy przejść do wstawienia ich w układ
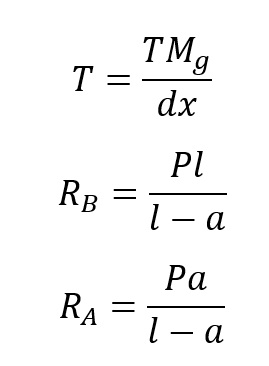
Od prawej strony zgodnie z odcinaniem belki w przekrojach charakterystycznych, takich przed którymi nie występują inne siły. Rozkładamy układ złożony na prostsze elementy.
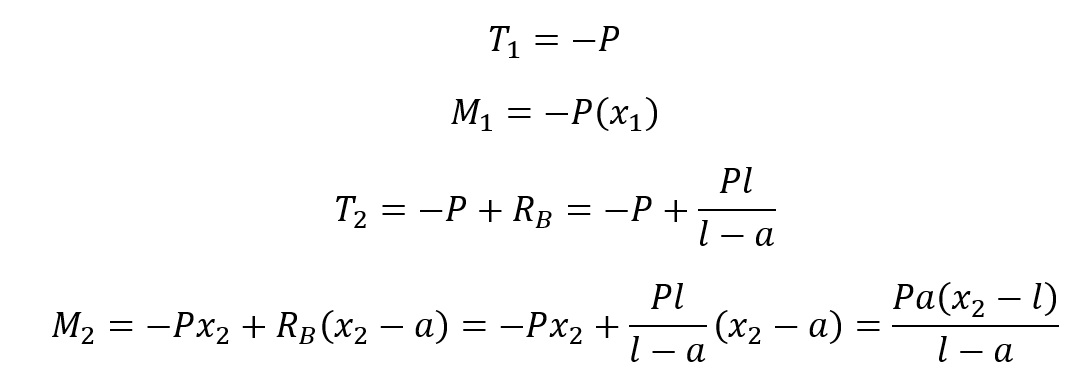
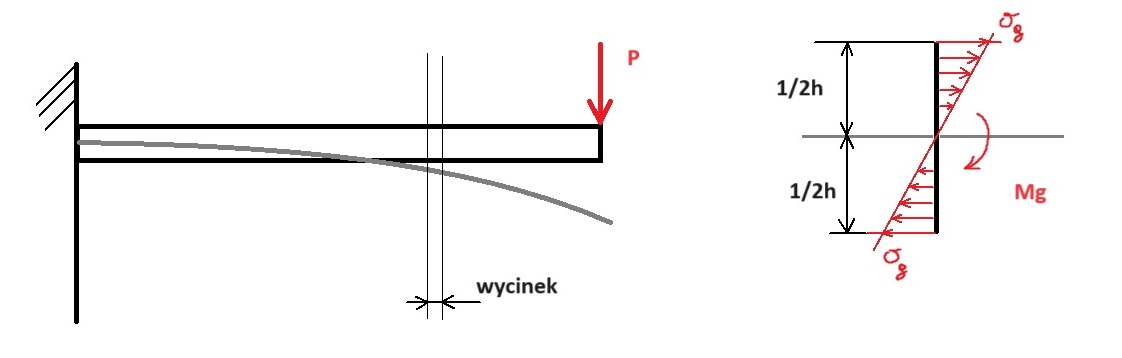
Naprężenia w pręcie zginanym
Wskaźnik Wytrzymałości przekroju na zginanie w osi obojętnej zginania przechodzącej przez oś z.
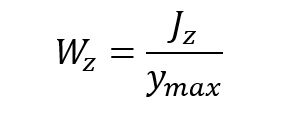
J_z – Moment bezwładności przekroju w osi Z.
y_max = 1/2h – jest najdalszym zginanym włóknem od osi obojętnej zginania
Naprężenia zginające (mające charakter naprężeń rozciągających bądź ściskających):
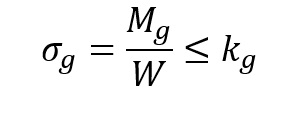 Wskaźnik Wytrzymałości przekroju na zginanie w osi obojętnej zginania
Wskaźnik Wytrzymałości przekroju na zginanie w osi obojętnej zginania
Gdzie k_g – naprężenia dopuszczalne na zginanie
Układy statycznie niewyznaczalne – równania i przykład
Dla układów statycznych wyznaczalnych tzn. nie przesztywnionych, reakcje można było wyznaczyć na podstawie równań statyki ciała doskonale sztywnego. Nie działa to jednak w przypadku układów dla których istnieje więcej reakcji (niewiadomych) niż warunków równowagi statycznej.
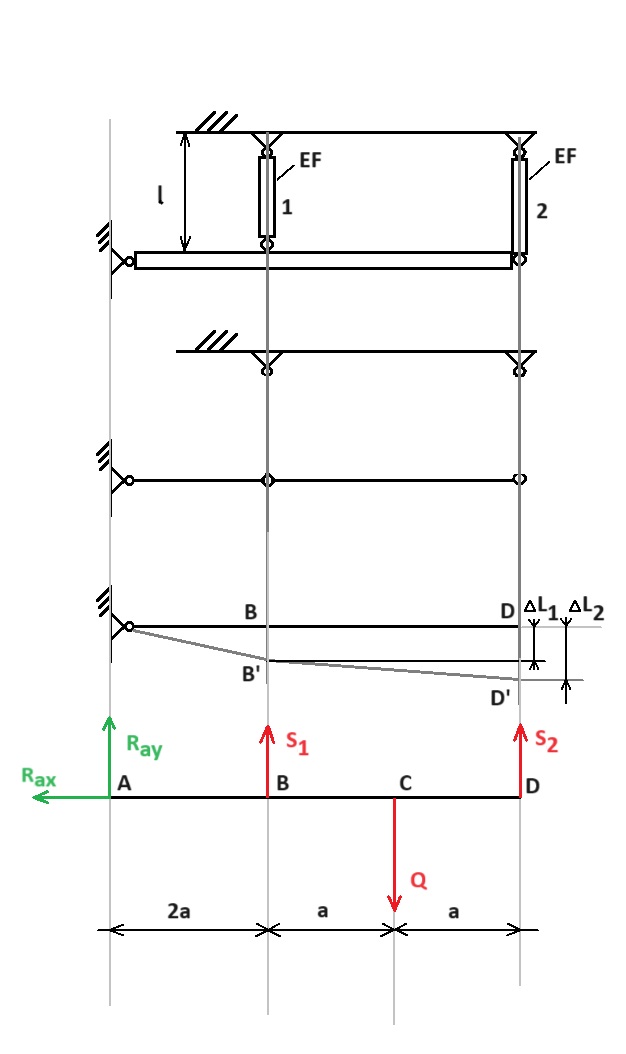
Równania równowagi :
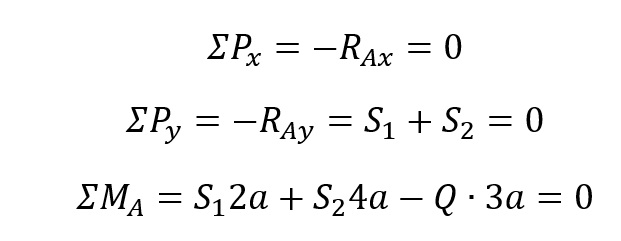
Brakujące równanie otrzymamy ze stosunku odkształceń, gdyż dla układów przesztywnionych to właśnie one odpowiadają za reakcje.
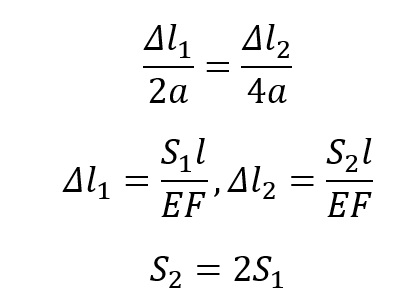
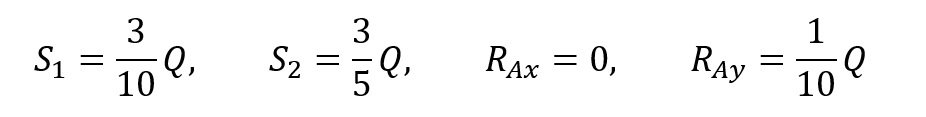
Wyboczenie prętów – objaśnienie i równania
Wyboczenie jest formą utraty stateczności. Wyboczenie może wystąpić w elementach smukłych, takich jak, pręty czy ściany, gdy naprężenia ściskające osiągną wartość krytyczną, powodując ich boczne wygięcie (wyboczenie) zamiast równomiernego ściskania.
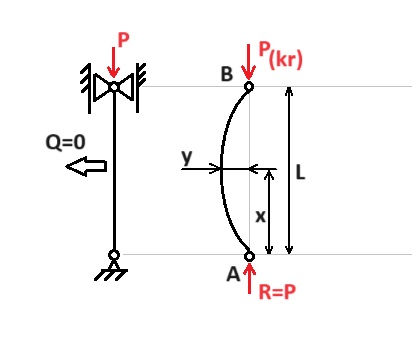
Wyboczenie prętów – czyli inaczej utrata stateczności pręta ściskanego
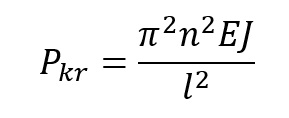
Gdzie
n = 1,2,3… (liczba naturalna)
E – moduł Younga materiału
J – moment bezwładności przekroju,
l – długość pręta, czasami oznaczana l_w
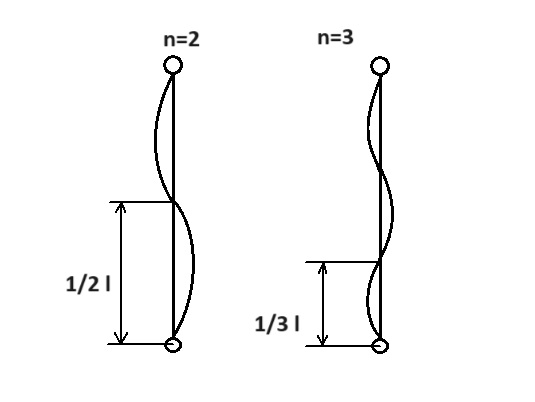
Krytyczną siłę ściskającą, która prowadzi do wyboczenia, można określić za pomocą wzoru Eulera dla idealnych warunków sprężystego wyboczenia:
| – wzór Eulera na krytyczną siłę ściskającą powodującą wyboczenie |
J_min – najmniejszy główny centralny moment bezwładności przekroju poprzecznego pręta
Naprężenie krytyczne przyjmuje postać
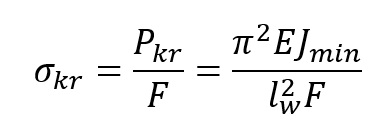
| – minimalny promień bezwładności przekroju | |
 |
– wymiar harakterystyczny pręta |
Zatem Krytyczne naprężenie ściskające, które prowadzi do wyboczenia, można określić za pomocą wzoru:
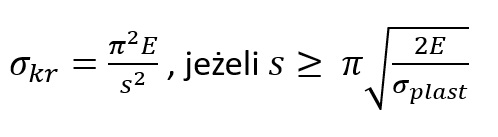
wzór Johnsona Ostenfelda