Moment dokręcania śrub i inne obliczenia połączeń śrubowych
Spis treści
Wymagany moment dokręcania śrub
Tarcie w złączu śrubowym
- Prawa Tarcia Coulomba:
Dobór gwintu
Siły działające w gwincie podczas dokręcania nakrętki:
- Warunek samohamowności śruby
Samohamowność gwintu
Napięcie wstępne w śrubie
Obliczenia Połączenia śrubowego równoległego
przykład obliczeniowy
Wymagany moment dokręcania śrub
Aby obliczyć moment dokręcania śruby należy zastosować poniższy wzór ogólny. Moment dokręcania śrub jest równy momentowi występującemu na gwincie oraz momentowi nakrętki/łba – w zależności czy przykręcamy za pomocą nakrętki czy na samej śrubie.
Mdokr = Mgwint + Mnakrętki
dalej będziemy używać oznaczeń
Mgwint = Mg
Mnakrętki = Mn
gdzie:
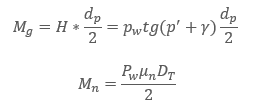
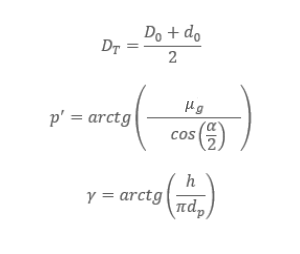
| D_T/2 | – uśredniona średnica tarcia |
μn – współczynnik tarcia nakrętki (między nakrętką a podstawą połączenia [blachą])
μg – współczynnik tarcia gwintu (między gwintem nakrętki a gwintem śruby)
D0 – maksymalna średnica działania siły
d0 – średnica otworu
Wymagany moment dokręcenia śruby (lub wymagany moment dokręcenia nakrętki) Mdokr – to moment który musi zostać przyłożony do łba śruby, lub nakrętki, jaki da nam siłę napięcia wstępnego (rozciągnie nam śrubę z siłą) Pw.
Momenty dokręcania śrub metrycznych dla różnych wielkości i klas – tabela momentów
Przy dokręcaniu śrub na wymagany moment należy zwrócić uwagę na 3-5% niepewności związanej z konstrukcją klucza dynamometrycznego. Dla konstrukcji bardzo odpowiedzialnych zaleca się przeprowadzanie szczegółowych obliczeń na moment dokręcenia śrub
| Średnica | Momenty dokręcania śrub w Nm | ||||
| Klasa: | 4.6 | 5.6 | 8.8 | 10.9 | 12.9 |
| M4 | 1 | 1,4 | 3,3 | 4,8 | 5,6 |
| M5 | 2 | 2,7 | 6,5 | 9,5 | 11,2 |
| M6 | 3,5 | 4,6 | 11,3 | 16,5 | 19,3 |
| M8 | 8,4 | 11 | 27,3 | 40,1 | 46,9 |
| M10 | 17 | 22 | 54 | 79 | 93 |
| M12 | 29 | 39,0 | 93 | 137 | 160 |
| M14 | 46 | 62 | 148 | 218 | 255 |
| M16 | 71 | 95 | 230 | 338 | 395 |
| M18 | 97 | 130 | 329 | 469 | 549 |
| M20 | 138 | 184 | 464 | 661 | 773 |
| M22 | 186 | 250 | 634 | 904 | 1057 |
| M24 | 235 | 315 | 798 | 1136 | 132 |
| M27 | 350 | 470 | 1176 | 1674 | 1959 |
| M30 | 475 | 635 | 1597 | 2274 | 2662 |
| M33 | 645 | 865 | 2161 | 3078 | 3601 |
| M36 | 1080 | 1440 | 2778 | 3957 | 4631 |
| M39 | 1330 | 1780 | 3597 | 5123 | 5994 |
| M42 | 1605 | 2006 | 4413 | 6285 | 7354 |
| M45 | 2005 | 2506 | 5512 | 7851 | 9187 |
Tarcie w złączu śrubowym
Zrozumienie działania i obliczania połączeń śrubowych należy zacząć od odpowiedniego zrozumienia mechanizmu przenoszenia siły w połączeniu. Głównym czynnikiem jest siła tarcia. Zarówno między gwintami śruby-nakretki jak i między głową śruby – podkładką i podkładką – blachą występują siły tarcia utrzymujące połączenie. W przypadku śrub luźnych siły tarcia dodatkowo przenoszą obciążenia. W przypadku śrub pasowanych czynnikiem utrzymującym statycznie połączenie także jest siła tarcia jednak obciążenia przenoszone są przez trzpień śruby. Moment dokręcenia śrub pasowanych także jest istotny z tego względu, że połączenie musi zostać statyczne nawet w przypadku wzmożonych wibracji.
Działem zajmującym się tarciem, smarowaniem i zużyciem powierzchni trących jest tribologia.
Podstawowym prawem opisującym zasadę działania tarcia statycznego są prawa tarcia kulomba
Prawa Tarcia Coulomba:
- Siła tarcia nie zależy od wielkości stykających się ze sobą elementów (pola powierzchni) – obecnie wiadomo, że to bzdura, jednak stanowi uproszenie na które możemy przymknąć oko z inżynierskiego punktu widzenia – ale zależy od ich rodzaju.
- Wartość siły tarcia ciała znajdującego się spoczynku może zmienić się od wartości zerowej do wartości granicznej wprost proporcjonalnie do nacisku normalnego.
- Gdy ciało jest w ruchu, siła tarcia na powierzchni styku, skierowana jest przeciwnie do kierunku ruchu i jest mniejsze od wartości granicznej.
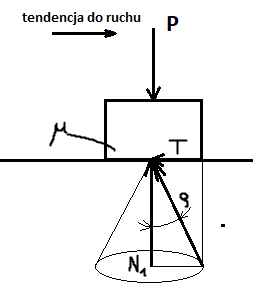
0 ≤ T ≤ Tmax
Tmax = μ · N
Gdzie:
N – siła normalna
μ – współczynnik tarcia
Warto nadmienić, że dla obliczeń statycznych wytrzymałości połączeń, będziemy rozważać przypadek dla granicznych sił tarcia z uwagi na to, iż jest to wartość, przy której układ po przekroczeniu przestaje być stabilny.
Kąt tarcia statycznego ρ=arctg(μ)
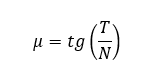
Śruby, według diagramu (i) różnią się sposobami przenoszenia sił, śruby pasowane przenoszą obciążenia całymi sobą, natomiast śruby luźne, służą do ściśnięcia elementów łączonych z taką siłą napięcia śruby, dla której siła tarcia między elementami łączonymi będzie wystarczająco wysoka, aby przeciwdziałać obciążeniom.
Dobór gwintu
Aby zacząć projektowanie połączenia śrubowego, należy określić jaki rodzaj gwintu chcemy zastosować. Ponizej przedstawono pięć prostych punktów krok po kroku jak określić jakiego gwintu potrzebujemy dla naszej aplikacji
- Rodzaj – Dobór gwintu zaczyna się od określenia rodzaju gwintu dla danego zastosowania. np. według naszego artykułu o gwintach, w którym poruszamy ową kwestię
Jeśli chcemy konstruować mechanizm śrubowy, najlepszym wyborem jest gwint trapezowy niesymetryczny lub symetryczny.
Jeśli chcemy aby połączenie było statyczne, najlepiej wybrać gwint samohamowny np. Gwinty zwykłe jednokrotne.
Jeśli chcemy aby połączenie było szczelne wybierami gwint calowy stożkowy samouszczelniający NPTF lub gwint stożkowy NPT. Należy przy tym pamiętać że gwinty NPT nie są samouszczeliające i należy stosować je z dodatkowym uzczelnieniem np. taśmą teflonową lub oringiem. Można także rozważyc użycie gwintu UNF lub BSP – także wymające dodatkowego uszczelnienia. Częstym rozwiązaniem dla gwintów UNF jest podkładka metalowo gumowa nazywana także podkładką DOWTY. - Średnicę gwintu należy dobrać odpowiednio do warunków pracy.
Obliczenia wytrzymałościowe dla śruby luźnej definiujące średnicę rdzenia śruby: Śruba luźna– charakterystyka i warunki projektowe
Obliczenia wytrzymałościowe dla śruby pasowanej (shoulder screw) definiujące średnicę trzpienia: Śruba pasowana– charakterystyka i warunki projektowe
Oto główne czynniki mające wpływ na średnicę.
– Zniszczenie trzpienia śruby- zerwanie śruby luźnej. Przy doborze średnicy gwintu należy patrzeć przedewszystkim na wytrzymałość połączenia. Jeśli zapewnienie wytrzymałości wymaga wprowadzenia dużego napięcia wstępnego śruby to średnicę należy dobrac odpowiednio dużą gwintu aby rdzeń wytrzymał i nie nastąpiło przekroczenie dopuszczalnych naprężeń rozciągających w śrubie luźnej lub naprężeń ścinających w śrubie pasowanej co prowadzi trzpienia śruby.
– Utracenie stateczności – zwłaszcza dla śrub długich (np. w szpilek w korpusie silnika) należy wziąć pod uwagę możliwość wyboczenia śrub. Więcej o wyboczeniach dowiesz się z artykulu z naszego działu o wytrzymałości materiałów
– Miejsce. Aby odpowiednio zaprojektować połączenie należy przeprowadzić „trade off” to znaczy rachunek zysków i strat związanych z wytrzymałością połączenia a masą, i rozmiarem połączenia. Zgodnie z zasadami dotyczącymi rozstawienia śrub w szeregach, śruby muszą znajdować się w odpowiednim położeniu i w odpowiedniej odległości od krawędzi materiału. Ma to wpływ nie tylko na stateczność połaczenia ale także na wzrosty naprężeń w miejscu, w którym śruba jest zbyt blisko krawędzi.
- Skok gwintu– ze względu na wymagane przełożenie mechaniczne, w przypadku korzystania z mechanizmów różnicowo-sumowych. Skok gwintu określa także czy gwint jest drobno czy grubo zwojny. Drobno zwojne gwinty mają większą średnicę rdzenia co za tym idzie większą wytrzymałość.
- Minimalne ramię klucza/pokrętła. Należy uważać aby odpowiednio dobrać ramię klucza dla danej siły. Częstym błedem przy montażu jest przekręcanie śrub do grnaic ich możliwości lub stosowanie przedłużeń klucza w formie rurki (ZDECYDOWANIE NIE ZALECAMY TAKIEJ METODY). Nie jest to najlepsze rozwiązanie nie tylko ze względu na wytrzymałość statyczną i olbrzymie siły rozciągające rdzeń śruby ale także na wytrzymałość zmęczeniową połączenia. Zbyt duzy moment dokręcenia może przesztywniać układ i prowadzić do przedwczesnychzniszczeń.
Przeciętny mężczyzna dysponuje około 300N siły w jednej ręce bez zapierania się, zalecamy projektowanie połączeń tak, aby uwzględniać ramię klucza mieszczącego się w normach. Duże momenty wmagają odpowiednich narzędzi np. elektrycznych lub hydraulicznych kluczy dynamometrycznych.
- Minimalna wymagana wysokość nakrętki śruby. W przypadku połączeń mocno wytęrzonych stosowne jest przeliczenie wysokości nakrętki i dobranie nie mniejszej z odpowiedniego katalogu według danego standardu (normy). Normy z nakrętakmi znajdziesz w naszym artykule dotyczącym rodzajów konstrukcyjnych śrub.
![]()
gdzie:
dM – średnica nominalna gwintu śruby
ηZW – wartość współczynnika współpracy zwoju nakrętki i śruby
h – skok gwintu
D1 – średnica wewnętrzna gwintu nakrętki
Siły działające w gwincie podczas dokręcania nakrętki:
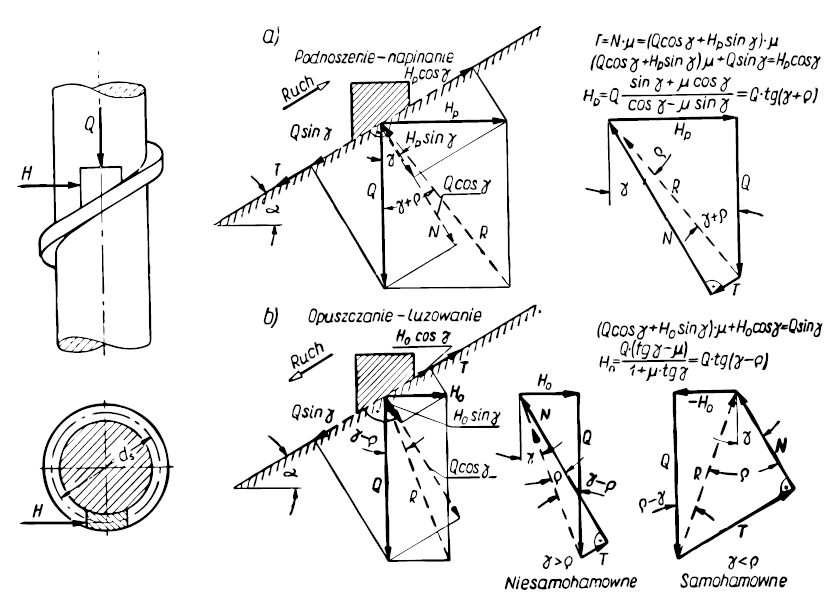
Pw – siła napięcia wstępnego (siła rozciągająca śruby)
Siły działające w gwincie podczas dokręcania nakrętki:
γ – kąt wniosu nakrętki
H = P·tg(p’+γ)
P – siła aktualnego napięcia śruby
N – siła normalna z jaką gwint oddziaływuje na zwoje nakrętki
T – siła tarcia
H – siła pozioma (prostopadła do osi śruby), którą trzeba przyłożyć do nakrętki (śruby) na średnicy podziałowej, dp żeby uzyskać równowagę sił.
p’ – kąt tarcia
γ – kąt wzniosu gwintu (nachylenia linii śrubowej)
Warunek samohamowności śruby:
aby gwint był samohamowny przy dokręcaniu śruby musi być spełniony warunek
H = P · tg(p’ – γ)
Dla innego kąta natarcia (gwint który nie jest prostokątny) odpowiada rysunek pod wzorami:
W takim gwincie występuje pozorny kąt tarcia (uwzględniający kąt zarysu śruby):
T’ = T = μN
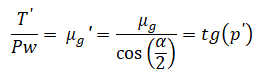
Mg – moment na gwincie
Mn – moment nakrętki
α – kąt zarysu gwintu stożka
μ_g – współczynnik tarcia gwintu
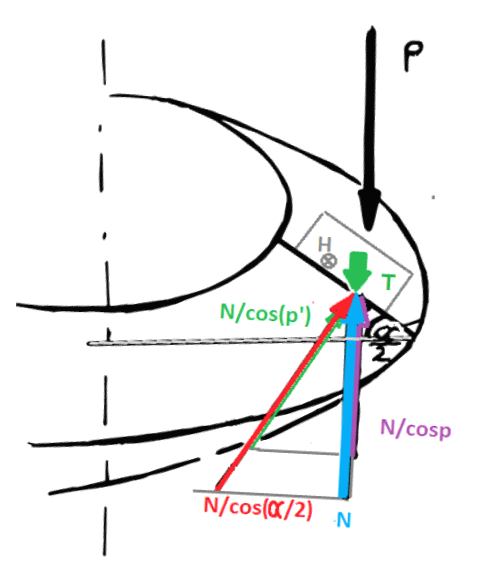
Samohamowność gwintu
Samohamowność – to właściwość układu, w której opór tarcia statycznego przeciwdziałający przesunięciu lub skręceniu wzajemnym powierzchni, zapewnia statyczność układu.
Dla gwintów Samohamowność występuje, gdy pozorny kąt tarcia p’ jest większy od kąta nachylenia linii śrubowej γ
H = p · tg(p’ – γ) > 0 → p’ > γ → gwint samohamowny
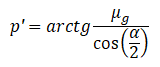
μg – współczynnik tarcia statycznego między oboma gwintami
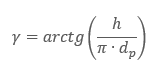
Żródła:
1. J.Dietrych, Podstawy Konstrukcji Maszyn II, Wydawnictwo Naukowo Techniczne – Warszawa
2. Witold Korewa, Części maszyn, część II, Państwowe wydawnictwo naukowe 1969
Napięcie wstępne w śrubie
Napięcie wstępne w śrubie wprowadza się w celu wywołania sprężystego rozciągnięcia śruby luźnej [i] generującego siły nacisku na powierzchnie łączonych elementów.
Bardzo ważna jest kontrola naprężeń, ponieważ poprzez odpowiednią kontrolę, można zmniejszyć naprężenia w śrubie wydłużając jej żywotność i uzyskując taką samą siłę napięcia zapewniającą wytrzymałość złącza.
Wymagany efekt może być uzyskany (kontrolowana wymagana siła napięcia wstępnego Pw) poprzez:
- kontrolę momentu dokręcenia nakrętki/śruby – klucze dynamometryczne
- kontrola siły w śrubie -rozciągnięcie wstępne śruby specjalnym urządzeniem, następnie przykręcenie nakrętki
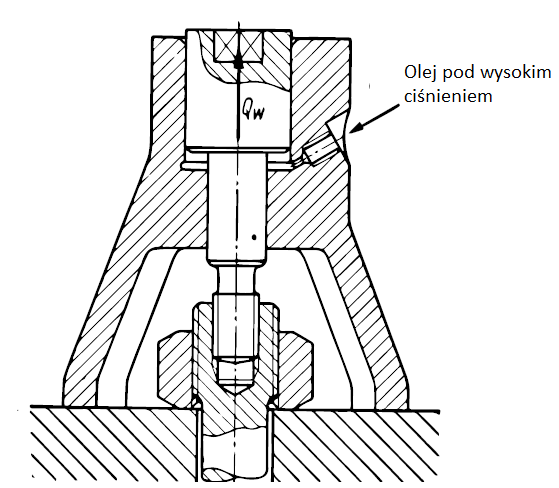
Schemat hydraulicznego urządzenia do napinania wstępnego śrub bez wywołania ich skręcania. Kontrola wydłużenia śruby pod wpływem Pw.
Czasami stosuje się także śruby ze znacznikiem napięcia wstępnego.
można także stosować łączniki śrubowe z innych materiałów takich jak:
- stale nierdzewne
- materiałów ceramicznych
- tworzyw sztucznych
- innych materiałów nieżelaznych

Łaczniki superbolt –brak naprężeń skręcających –brak współczynnika f.
Przykład obliczeń Połączenia śrubowego równoległego z momentem dokręcania śrub
Treść : Wspornik traktowany jako metalowa konstrukcja skręcana. Połączenie widoczne na rysunku uzyskane jest za pomocą śrub luźnych. Wyznaczyć:
Potrzebne napięcie wstępne w śrubach
Średnicę nominalną śrub z gwintem metrycznym zwykłym
Wymagany moment dokręcenia przy zał. Wsp. Tarcia (μ , μg)
Minimalna długość ramienia klucza
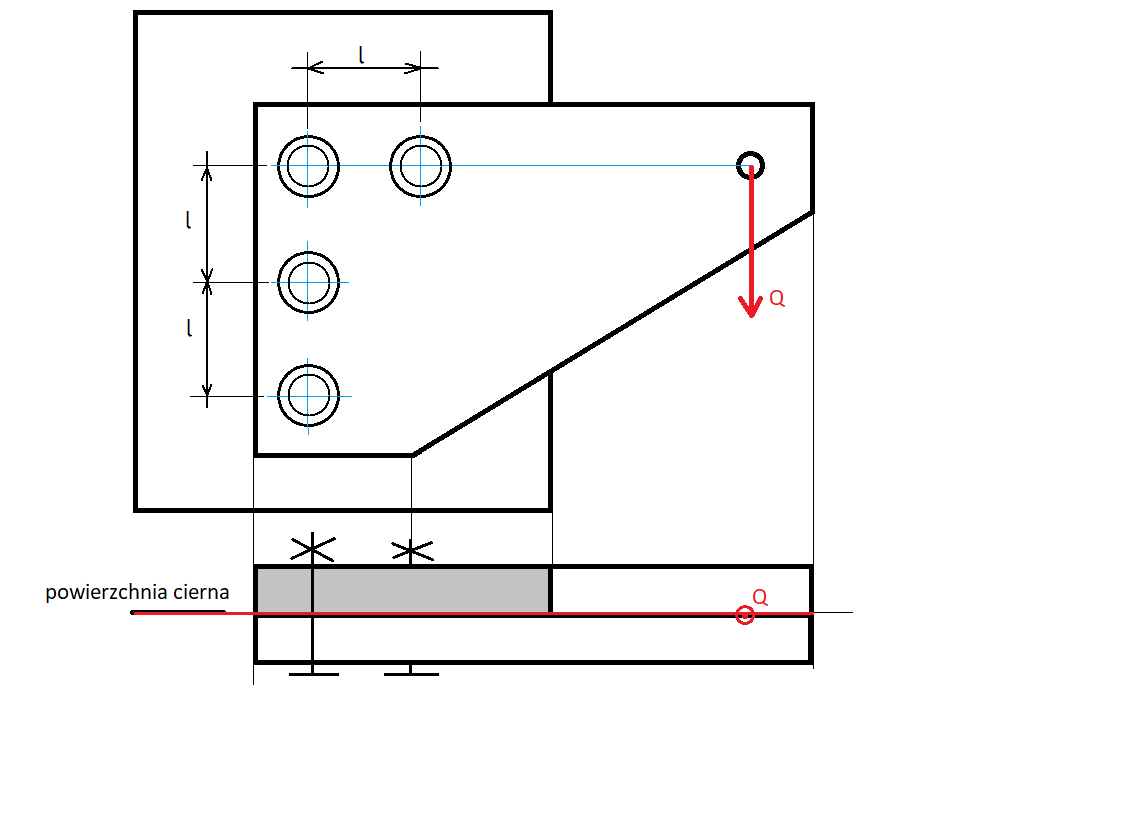
Dane:
Q, L, l, Re, x,
n_śrub – liczba śrub
i_powierzchni ciernych – liczba powierzchni ciernych,
F_ręki – siła ręki (siła ręki mężczyzny to około 300N),
μ = 0,1 – wzpółczynnik tarcia na blachach
μg = 0,1 – wzpółczynnik tarcia na gwincie
X=2,0 – współczynnik bezpieczeństwa
do= dn + 3mm – zakładana średnica otworu pod śrubę
Z uwagi na dokręcenie śrub kluczem, obowiązuje współczynnik skręcenia f=1,3
Klasa śrub 8,8
Na początku należy wprowadzić uproszczony model i z rysunku wyznaczyć schemat obciążenia.
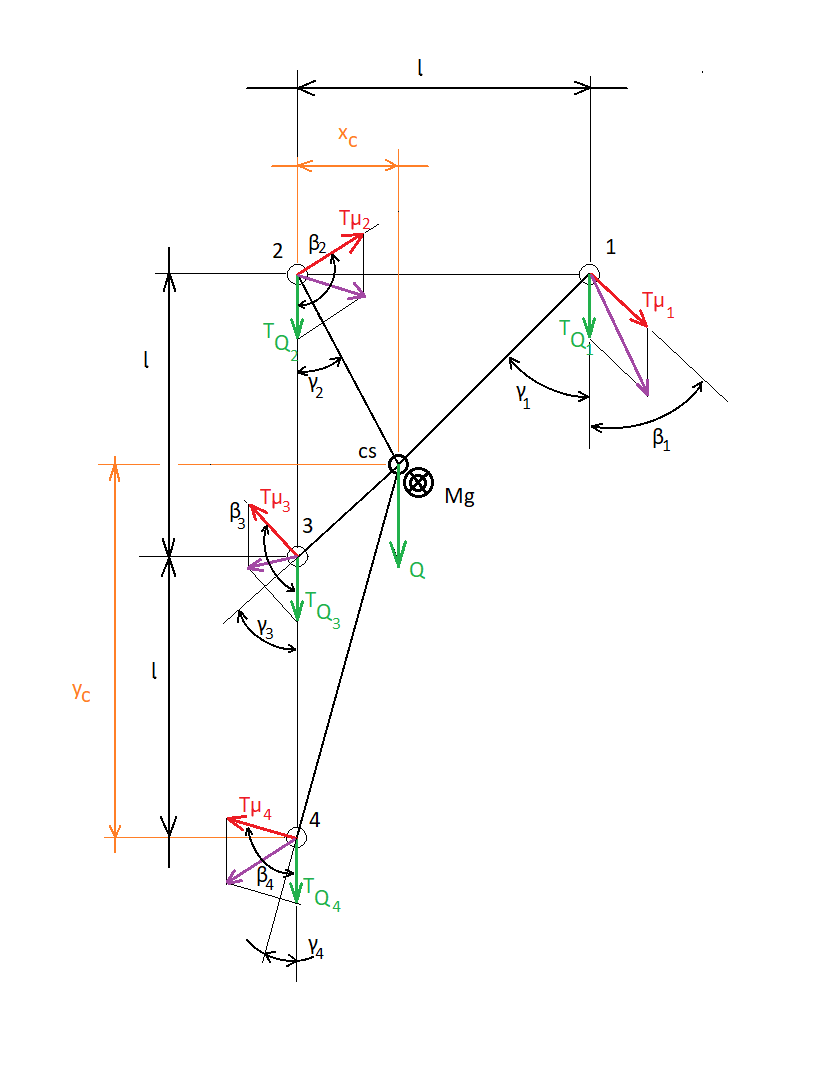
Obliczenia sił i momentów działających na wspornik :
Pierwszym krokiem jest przeniesienie sił do środka ciężkości połączenia
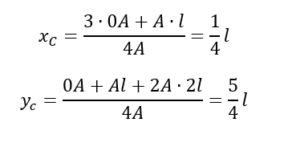
Następnie liczymy momenty i siły działające na śruby

Promienie działania sił:
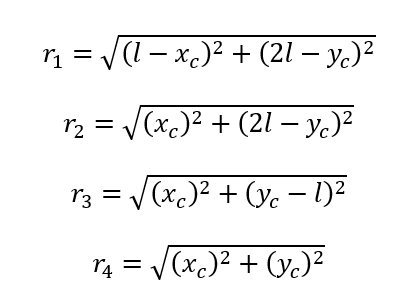
Szukamy najbardziej obciążonej śruby
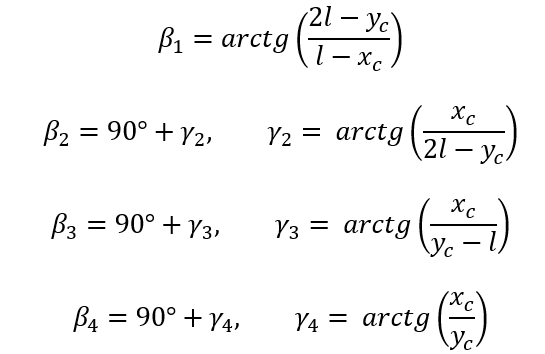
Najbardziej obciążona śruba, to śruba dla punktu 1.
Z twierdzenia cosinusów
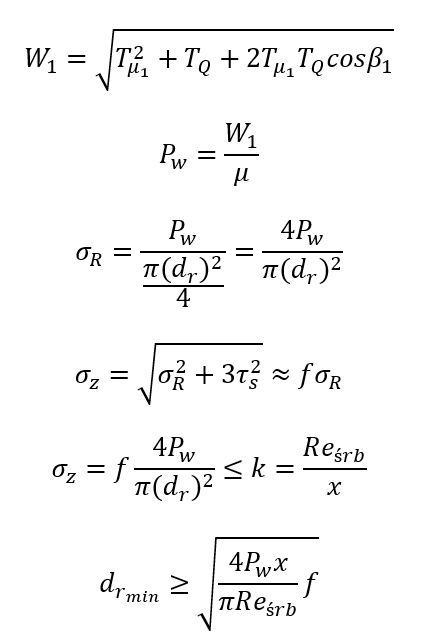
Gdzie
(d_r)_min – minimalna średnica rdzenia śruby – na jej podstawie możemy dobrać średnicę nominalną śruby dn
Następnie obliczamy moment dokręcenia śruby/nakrętki
M_dokr – Wymagany moment dokręcenia
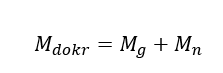
M_g = Moment występujący na gwincie
M_n = moment występujący na nakrętce
W takim przypadku wzory do zastosowania w przypadku wyliczania momentu dokręcenia nakręrtki dla śruby wypisane są poniżej
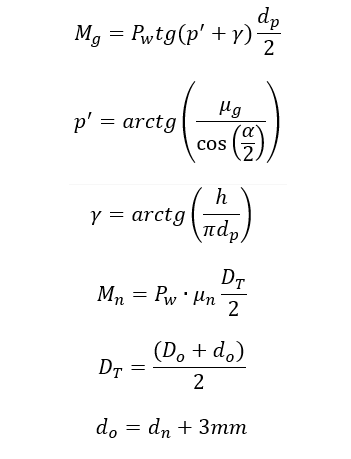
μ_g- współczynnik tarcia gwintu
dn – średnica nominalna
D_T – średnica działania siły tarcia na nakrętce według oznaczeń
Zatem moment dokręcenia nakrętki dopuszczalny dla klucza ręcznego wynosi
R_min – minimalna długość klucza
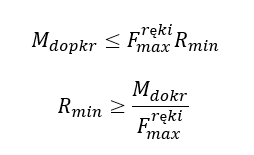
Długość klucza może wynieść nawet parę metrów. Nie oznacza to, że klucz musi być taki długi, oznacza natomiast, że należy przykręcić śrubę wkrętarką lub użyć klucza z przekładnią zapewniającą odpowiedni moment .
