Moduł Younga i statyczna próba rozciągania
Spis treści
Związki konstytutywne
Statyczna próba rozciągania, Granica sprężystości, plastyczności i inne
-
Granica proporcjonalności RH
-
Rsp – granica sprężystości
-
Re – granica plastyczności
-
Rm – wytrzymałość doraźna
-
Re_sy – Granica plastyczności przy ścinaniu (Fsy) Prawo Hooka
Moduły sprężystości; Younga, Kirhoffa i Liczba Poissona – wyjaśnienie wraz ze wzorami
-
Moduł Younga, E – moduł sprężystości podłużnej
-
Moduł Kirhoffa, K – hydrostatyczny moduł sprężystości
-
Liczba Poissona v, Współczynnik Poissona
Właściwości wytrzymałościowe materiału i bazy materiałowe
Moduł Younga, moduł Kirhoffa i Liczba Poissona – wyjaśnienie wraz ze wzorami
Moduł Younga –
czyli Moduł sprężystości podłużnej (ang. Young’s modulus), jest jednym z najważniejszych parametrów charakteryzujących materiały. Opisuje on w jaki sposób materiał zachowuje się (odkształca) pod wpływem naprężeń i odwrotnie. Jakie naprężenia mogą pojawić się w materiale przy zadanym odkształceniu.
W wytrzymałości materiałów używany jest jako miara sztywności materiału. Moduł Younga jest wykorzystywany do określenia, jak materiał zachowa się pod wpływem sił rozciągających lub ściskających, bez przekraczania granicy jego sprężystości, to znaczy zakresu, w którym materiał jest w stanie powrócić do swojego pierwotnego kształtu po usunięciu obciążenia – z pominięciem histerezy.
Moduł Younga określa tak zwaną proporcjonalność (czyli charakterystykę liniową) pomiędzy naprężeniami i odkształceniami w obszarze granicy proporcjonalności (liniowości odkształcenia i naprężeń). To zakres, w którym naprężenia rosną wprost proporcjonalnie do odkształceń.
Matematycznie Moduł Younga można zapisać w postaci
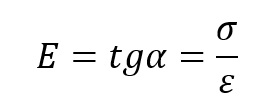
Gdzie α równe jest kątowi nachylenia linii wykresu funkcji σ =f(ε)
ε – odkształcenie
σ – naprężenie
Zwykle Moduł Younga wyrażamy w MPa (MegaPascal) lub GPa (GigaPascal) czyli [N/m²].
Tabela wartości Modułu Younga dla wybranych materiałów konstrukcyjnych.
| Materiał | Moduł Younga (E) |
| GPa | |
| Guma | 0,01–0,10 |
| Polistyren | 3,0–3,5 |
| Beton | ponad 25 (ściskany) |
| Stopy aluminum | około 70 |
| Miedź | 110–140 |
| Brąz | 105–120 |
| Tytan | 105–120 |
| Żeliwo i stal | 190–210 |
| Wolfram | 400–410 |
| Węglik krzemu (SiC) | 450 |
| Węglik tytanu (TiC) | około 650 |
| Diament | około 1100 |
Moduł Kirhoffa K
– hydrostatyczny moduł sprężystości –
Stosuje się go w przypadku obciązeń występujących z każdej strony.
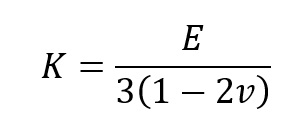
Dla ścinania i skręcania występuje moduł Kirhoffa oznaczany jako G nazywany modułem sprężystości poprzecznej lub modułem sprężystości postaciowej
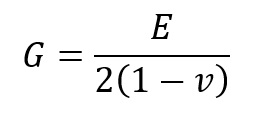
Gdzie v – Liczba Poissona
Liczba Poissona v,
współczynnik Poissona – jest to parametr opisujący stosunek odkształcenia poprzecznego do odkształcenia podłużnego przy jednoosiowym stanie naprężeń.

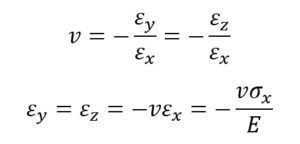
Liczba Poissona przyjmuje wartości od -1 do 0,5
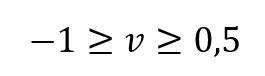
Związki konstytutywne
Związki konstytutywne – To główne zależności między składowymi tensora (wektora rozpostartego na powierzchni) naprężeń i tensora odkształceń opisujące dany materiał. Można powiedzieć, że jest to opis wzajemnego zachowania tych dwóch wielkości pozwalający nam przewidywać zachowania materiałów.
Dla ciał będących ciałami izotropowymi (posiadającymi w każdym punkcie takie same właściwości dla każdego kierunku), liniowo-sprężystym związkiem konstytutywnym jest prawo Hooka
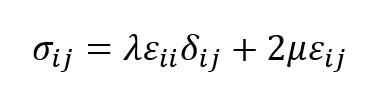
Gdzie:
δij – delta Kroneckera
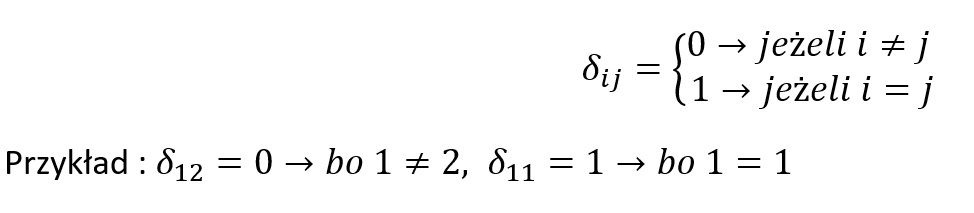
λ i µ – stałe Lamiego
Stała µ jest równa modułowi Kirchhoffa, można spotkać tradycyjny zapis G
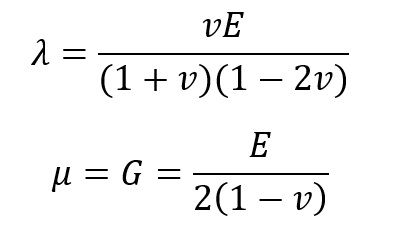
E – moduł Younga
V – liczba Poissona
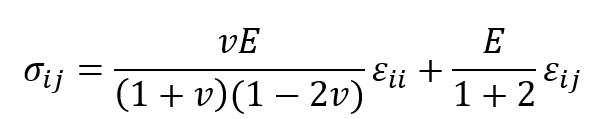
εii, εij – tensory odkształceń
Dla ciał plastycznych ze wzmocnieniem – tzn. takich dla których przy osiągnięciu granicy plastyczności, krzywa (lub prosta) naprężeń rośnie dalej, ale wolniej występuję zależność:
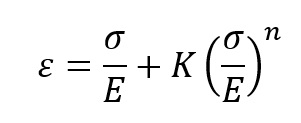
Gdzie :
ε – odkształcenie
σ – naprężenia
E – moduł Younga
K i n – stałe charakterystyczne dla danego materiału – pozyskane z danych eksperymentalnych
Dla pełnego opisu ciała potrzebne jest 9 składowych tensora naprężeń σ, 9 składowych tensora odkształceń ε i 3 składowe wektora przemieszczeń U. Z punktem przestrzeni nie są związane momenty sił, tzn. zachodzi zależność
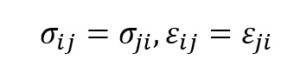
Zależności między składowymi tensora odkształceń i wektora przemieszczeń:
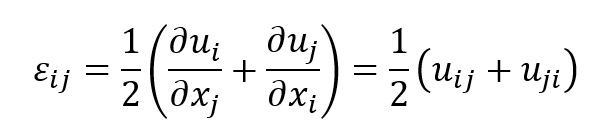
Co daje nam 12 równań.
Dodatkowe wymagane 3 równania otrzymamy z równania równowagi ośrodka ciągłego dla układów statycznych.
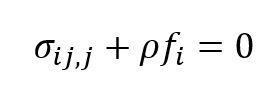
Gdzie :
fi – składowa wektora sił masowych
ρ – gęstość materiału
dla układów dynamicznych obowiązuje dodatkowo równanie zachowania pędu ośrodka ciągłego:
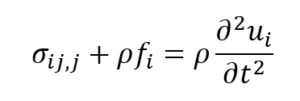
Statyczna próba rozciągania, Granica sprężystości, plastyczności i inne
Aby opracować poprawne współczynniki dla ogólnych równań z powyższych wzorów, związków konstytutywnych, wykonuje się próby wytrzymałościowe.
Podstawową próbą statyczną jest próba rozciągania materiału. Aby wyniki były porównywalne wprowadzono znormalizowane próbki, tak że kształt próbek i ich liczba zależy od normy, na którą się powołujemy. Dla materiałów sprężysto plastycznych można jednak wyprowadzić wspólną zależność. Próbki dla materiałów plastycznych są długie walcowe i smukłe natomiast dla materiałów kruchych próbki są walcowe i krótsze.
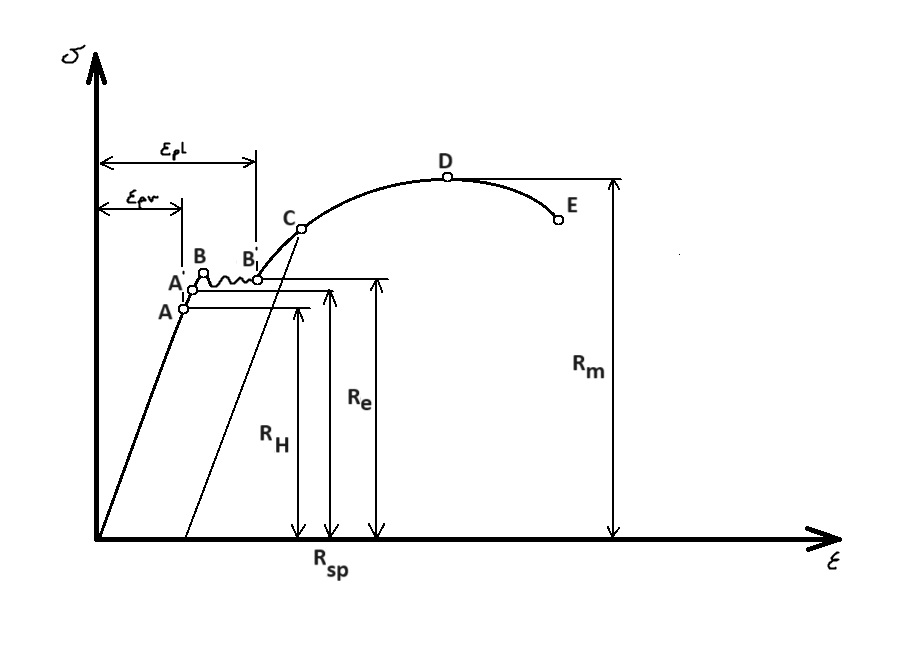
Wynikiem prób wytrzymałościowych na rozciąganie zazwyczaj jest wykres naprężeń w funkcji odkształcenia opisujący funkcję:
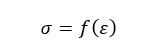
Tzn. opisuje zależność wydłużenia od siły rozciągającej odniesionej do naprężeń
Granica proporcjonalności RH – od nazwiska Hooka – jest to naprężenie w materiale przy którym występuje jeszcze liniowa odkształcalność tzn. zależność między naprężeniami a odkształceniem jest liniowa.
Rsp – granica sprężystości – są to naprężenia przy których liniowość już nie występuje, ale po odciążeniu próbka wraca do swoich pierwotnych wymiarów i nie występuje wyraźne, trwałe odkształcenie próbki. Zazwyczaj Rsp i RH są tożsame ze względu na bardzo bliskie położenie na wykresie
Re – granica plastyczności – są to naprężenia przy których zachodzi uplastycznienie materiału tzn. występuje wzrost odkształceń przy stałym naprężeniu. Jeśli w danym materiale nie występuje wyraźna granica plastyczności to stosuje się umowną granicę plastyczności Re_0,2. Jest to taki punkt wykresu w którym odkształcenia trwałe osiągają wartość 0,2% wartości początkowej
Punkt B’ – Umocnienie materiału, punkt w którym poślizgi warstw kryształów materiału ulegają zahamowaniu i od tego momentu należy zwiększyć naprężenia w celu wywołania odkształceń. Nie jest obecny dla każdego materiału.
Rm – wytrzymałość doraźna (Punkt C) – Naprężenia przestają być jednorodne, występuje koncentracja poślizgów w jednym miejscu. Jest to punkt w którym naprężenia są największe
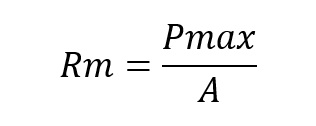
Gdzie A – pole nominalne (początkowe) próbki
Efekt umocnienia materiału wykorzystuje się w technice w celu podwyższenia wytrzymałości materiału. Jeśli rozciągniemy próbkę do puktu E i następnie odpuścimy, to próbka zachowywać się będzie jak sprężysta gdzie granica sprężystości przesunie się do punktu E.
Warto pamiętać, że aby mieć jasny ogląd na właściwości wytrzymałościowe danego materiału należy wykonać więcej niż jedną próbę rozciągania w więcej niż jednym kierunku.
Re_sy – Granica plastyczności przy ścinaniu (Fsy) – zazwyczaj pozyskiwana z testów skręcania zależy od kształtu próbki.
Dane pozyskiwane są z :
1. Dla blach – testów przebicia
2. Dla kształtowników o dużych przekrojach – ścianie ze sworzniem
Dodatkowo może być oszacowana w oparciu o wytrzymałość na rozciąganie i ściskanie
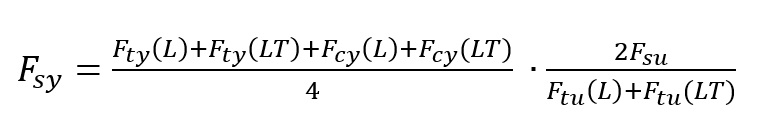
Gdzie
F_tu(L) – wytrzymałość na rozciąganie w kierunku L
F_tu(LT) – wytrzymałość na rozciąganie w kierunku LT
F_ty(L) – Granica plastyczności przy rozciąganiu w kierunku L
F_ty(LT) – Granica plastyczności przy rozciąganiu w kierunku LT
F_cy(L) – granica plastyczności przy ściskaniu w kierunku L
F_cy(LT) – granica plastyczności przy ściskaniu w kierunku LT
F_su – wytrzymałość na ścinanie
Prawo Hooke’a – Prawo mechaniki głoszące, że odkształcenia ciała pod wpływem działania na nie siły jest proporcjonalne do tej siły
Dla rozciągania statycznego pręta:
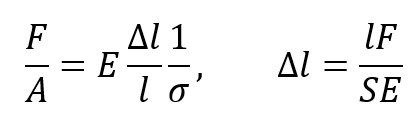
F – siła rozciągająca
A – Pole przekroju poprzecznego pręta
Δl – wydłużenie pręta
l – długość pręta
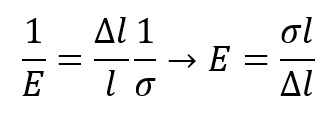
Lub
![]()
Gdzie :
ε=Δl/l – odkształcenie
σ=F/A – naprężenie
Właściwości wytrzymałościowe materiału i bazy materiałowe
Każdy materiał w swojej definicji ma przedziały procentowe zawartości danego pierwiastka. Mimo, ze te wartości są ściśle określone – w tym parametry wytrzymałościowe to zawsze istnieją rozbieżności od wartości przewidywanych. W celu określenia jak definiować wartości właściwości wytrzymałościowych w taki sposób aby były one jak najbardziej przewidywalne a zarazem jak najlepsze wprowadzono bazy danych materiałowych. Są to statystyczne bazy opisujące prawdopodobieństwo uzyskania pewnych (takich do których mamy pewność) założonych parametrów projektowych.
Baza typowa – wartości wytrzymałościowe i innych parametrów materiału opisane są jako wartość średnia, z pominięciem oceny statystycznej.
Baza typu S – S basis value – wartości własności materiału określane sa przez minimalne wartości podane w normach.
Baza typu B – B-basis value – baza opisuje takie wartości parametrów materiałów, że dla 90% populacji były one większe lub równe od statystycznej wartości, dla poziomu ufności 95%. To oznacza, że z 95 procentową pewnością 90% danego materiału posiada lepsze lub równe właściwości od wartości statystycznej (np. założonej Re_min)
Baza typu A – A-basis value – baza opisująca takie wartości parametrów materiałowych, że dla 99% populacji wartości są równe lub przekraczają statystyczne wartości dla poziomu ufności 95%. To oznacza, że z 95 procentową pewnością 99% danego materiału posiada lepsze lub równe właściwości od wartości statystycznej (np. założonej Re_min).
Wartości w A-basis są zazwyczaj niższe niż wartości B-basis, jednak decydując się na założenie wartości parametrów z bazy A, mamy większą kontrolę nad pewnością zachowania materiału w warunkach roboczych.