Podstawy wytrzymałości materiałów
Spis treści
Wytrzymałość materiałów
Stany naprężeń
Rodzaje obciążeń
Odkształcenie
-
Odkształcenie całkowite
-
Odkształcenie rzeczywiste
-
Współczynnik koncentracji odkształceń
-
Odkształcenie obiętościowe
Naprężenie
Analiza naprężeń i odkształceń
Rysowanie koła Mohra
Czym jest Wytrzymałość materiałów
Wytrzymałość materiałów – to dziedzina nauki zajmująca się opracowywaniem oraz analizą metod oceny zachowania elementów konstrukcyjnych pod wpływem obciążeń. Podstawy wytrzymałości materiałów obejmują zagadnienia związane z głównymi parametrami są odkształcenia i naprężenia. W celu przewidywania zachowania danych konstrukcji należy wykonać model tej konstrukcji. W zależności od dokładności z jaką chcemy przewidzieć zachowanie, możemy wybrać mniej lub bardziej dokładny model obliczeniowy.
Model konstrukcji zazwyczaj składa się z:
- Modelu matematycznego – obliczeń dokonuje się na podstawie wybranego kryterium wytrzymałościowego dla wybranej hipotezy wytężeniowej.
- Modelu materiałowego – według norm i badań
- Modelu geometrycznego – jako uzupełnienie do modelu matematycznego i materiałowego. Dla różnych metod obliczeniowych, stosuje inne modele geometryczne. Model analityczny wymaga geometrii jednolitej natomiast model obliczeniowy FEM (pl. MES) wymaga dyskretyzacji modelu geometrycznego.
W celu utworzenia stabilnych zależności (zależy nam na tym, ponieważ każda próbka materiału jest unikatowa) wprowadzono pewne uproszczenia, które mają zastosowanie jedynie w przypadku materiałów liniowo sprężystych – to znaczy takich które są sprężyste (wywierają siłę reakcj) proporcjonalnie do odkształcenia. W podstawach wytrzymałości materiałów często stosuje się uproszczenia aby zniwelować wpływ czynników losowych takie jak:
- Ciągłość materiału – założenie polegające na koncepcji materiału jednorodnego Stal żeliwa aluminium stopy miedzi polimery itp. Nie mają jednolitej struktury, posiadają one liczne wewnętrzne defekty, wtrącenia, puste przestrzenie i nieciągłości nie dające się przewidzieć. Dlatego takie założenie ma sens z matematycznego punktu widzenia jednak nie ma przełożenia na rzeczywistość.
- Jednorodność materiału – jest następstwem pierwszego założenia. Właściwości materiału nie są zależne od położenia w materiale co za tym idzie, właściwości materiału są takie same w każdym jego punkcie. Nie sprawdza się przy gradientach temperatur i spiętrzeniach naprężeń
- Izotropowość materiału – założenie, że materiał posiada takie same właściwości w każdym kierunku (osi) objętości ciała. W rzeczywistości tak nie jest i nawet sposób obróbki materiału może mieć wpływ na kształt i ułożenie ziaren kryształów materiału tym samym zmieniając parametry w danym kierunku.
- Liniowa sprężystośc materiału – założenie, że istnieje pewien bazowy, bezobciążeniowy stan ciała, do którego ciało dąży po odpuszczeniu obciążeń a w trakcie których, do pewnego stopnia, ciało zachowuje ciągłość struktury.
Stany naprężeń
Stany naprężeń dzielimy na :
Jednoosiowy stan naprężeń – gdy uczestniczy w nim jedno napręzenie główne σ1 a dwa pozostałe wynoszą 0. Występuje on między innymi w
Dwuosiowy stan naprężeń– gdy obecne naprężenia σ1 i σ2 w dwóch osiach zwany także pod inną nazwą płaski stan naprężeń. Taki stan występuje (oczywiście w akceptowalnym przybliżeniu) na przykład w elementach dwuwymiarowych w których wymiar głębokości można pominąć. Płaski, dwuosiowy stan naprężeń występuje w skorupach zbiorników, poszyciu pojazdów lub płaskownikach.
Trójosiowy stan naprężeń – gdy obecne są naprężenia σ1, σ2 i σ3 w trzech osiach. Występuje w elementach kórych nie można pominąć wymiaru głębokości, np. wsporniki, wachacze w pojazdach lub korpusy silników.
Jeśli naprężenia główne są sobie równe to mamy do czynienia z hydrostatycznym stanem naprężeń, gdy naprężenia na każdej ścianie elementu są jednakowe, naprężenia takie zmieniają objętość bryły lecz nie zmieniają jej kształtu (postaci)
Tensor główny naprężeń można zapisać jako
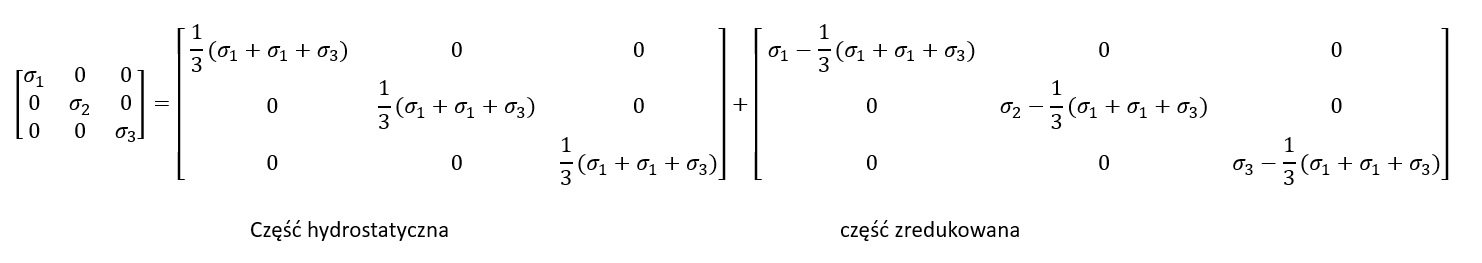
Składowa zredukowana (naprężenia zredukowane) nie zmienia objętości ciała ale za to zmienia jego postać. To właśnie napręzenia zredukowane odpowiadają, za zniszczenie elementu. Napręzenia zdedukowane odpowiadają także za płynięcie plastyczne materiału.
Rodzaje obciążeń
Podstawy wytrzymałości materiałów opisują także zachowanie obciążenia. Obciążenia to inaczej siły zewnętrzne działające na ciało które dzielimy na:
- Stałe obciążenia zwane także obciążeniami statycznymi
- Zmienne obciążenia zwane inaczej obciążeniami dynamicznymi
- Pracy
- Otoczenia
- Transportowe i montażowe
Gdzie:
Obciążenia stałe to obciążenia niezmienne w czasie. Zazwyczaj odpowiadają za nie ciężar własny konstrukcji oraz ciężar elementów podtrzymywanych.
Obciążenia zmienne to obciążenia nie stałe w czasie.
Obciążenia wynikające z pracy to obciążenia zmienne wynikające z charakteru pracy układu. Należą do nich np. zmienne obciążenia wału, zmienne obciążenia urządzeń cieplnych (np. tłok w silniku spalinowym).
Obciążenia otoczenia to wpływ warunków w jakich pracuje konstrukcja np. wiatr, temperatura, promieniowanie.
Obciążenia transportowe i montażowe to obciążenia wynikające z procesu transportu np. wibracje, szoki oraz sposobu montażu np. osadzanie ciasno pasowanego łożyska na wale.
Dodatkowo możemy je podzielić na obciążenia proste
Naprężenie
Naprężenie – jest wielkością fizyczną która opisuje siły wewnętrzne wywierane przez sąsiednie cząstki materiału (ciągłego) wywierają na siebie. Opisuje się ją poprzez siłę działającą na danej powierzchni, zatem opisuje się ją poprzez orientację w przestrzeni i kierunek działania siły.
Równanie ogólne naprężenia
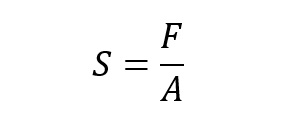
S – naprężenia na powierzchni
F – siła
A – Pole powierzchni
Zatem naprężenia fizycznie są siłą rozłożoną na danym polu powierzchni
Naprężenia w punkcie:
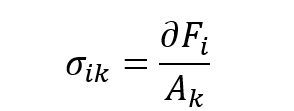
Naprężenia mogą być zarówno normalne (prostopadłe) do płaszczyzny jak i styczne (równolegle) do płaszczyzny.
Naprężenia normalne – rozciągające lub ściskające.
Naprężenia styczne – ścinające (tnące).
Naprężenia inżynierskie – stosunek siły F do przekroju poprzecznego początkowego na który działa siła.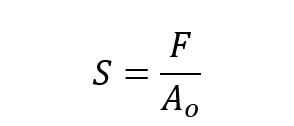
Przy założeniu że materiał odkształca się bez zmiany objętości.
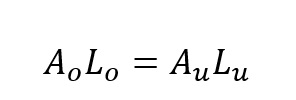
Ao – początkowe pole przekroju.
Lo– początkowa długość elementu.
Au– pole przekroju po odkształceniu.
Lu– długość elementu po odkształceniu – długość końcowa.
Naprężenia osiągają więc wartość:
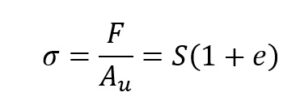
e – odkształcenia inżynierskie
S – naprężenia inżynierskie
K= σ/S – współczynnik koncentracji naprężeń
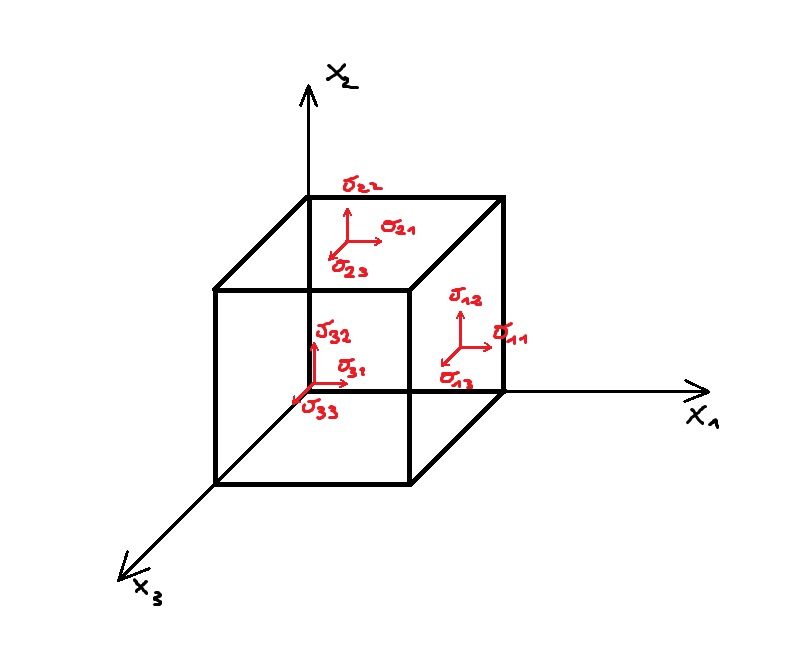
Naprężenia σ_ij są naprężeniami działającymi na ściany
| – naprężenia normalne | |
| – naprężenia styczne |
Sprowadzając element do punktu przestrzennego można utworzyć macierz zwaną tensorem naprężeń.
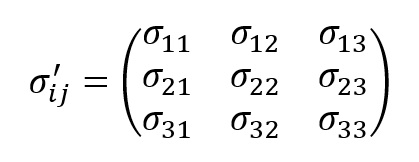
Naprężenia główne
Każdy układ tensorów na nieskończenie małym elemencie w układzie kartezjańskim da się sprowadzić i ustawić w taki sposób aby w danym zmodyfikowanym układzie występowały tylko naprężenia normalne do powierzchni elementu nazywane naprężeniami głównymi, gdzie tensor naprężenia w układzie współrzędnych wyznaczonym przez wektory własne:
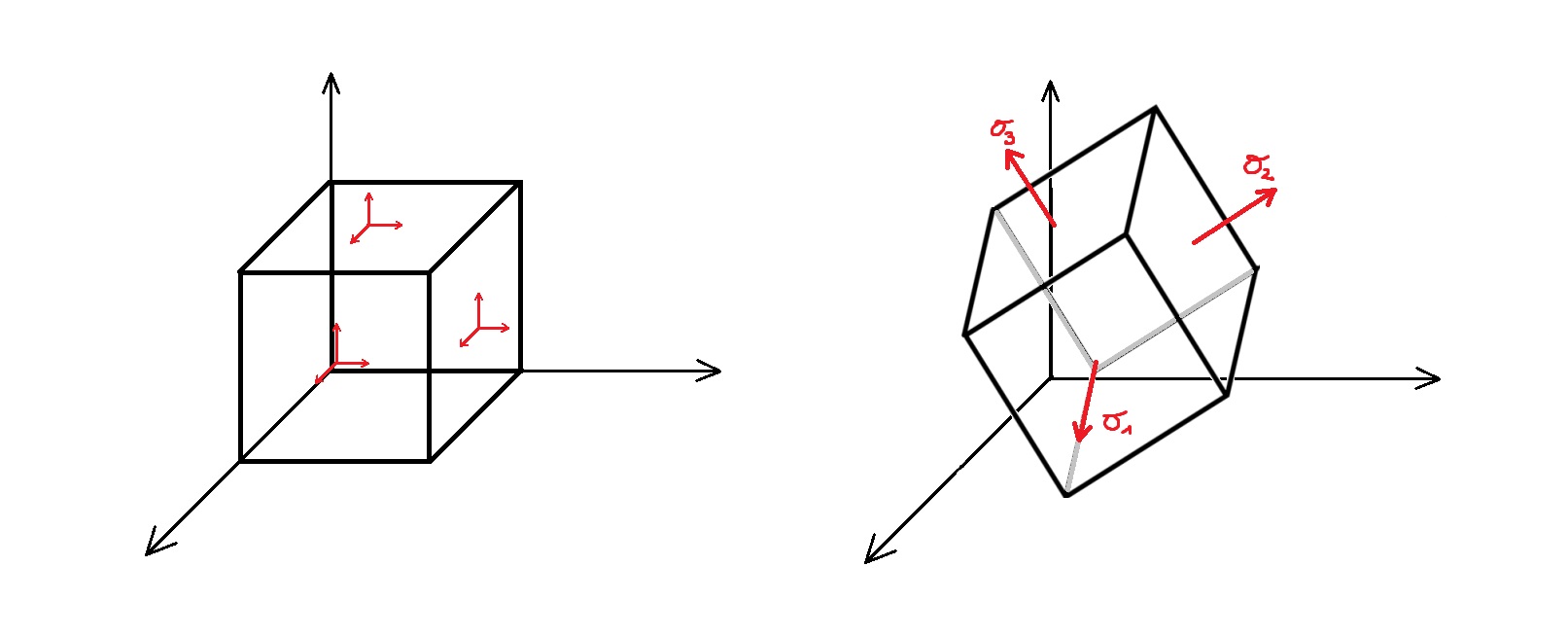
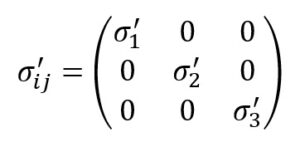
Umownie przyjęte zostało, że naprężenia główne porządkuje się w danej kolejności
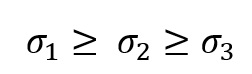
Naprężenia resztkowe
naprężenia w ciele, na które nie działają siły zewnętrzne pozostające w stanie równowagi w jednorodnej temperaturze. Naprężenia takie mogą być wynikiem wytwarzania lub obróbki (np., kucia) materiału. W celu pozbycia się tych naprężeń lub ich zredukowania stosuje się zabiegi odprężające. Jest to istotne w celu zachowania wysokich dokładności wykonania geometrii przedmiotu.
Odkształcenie
Odkształcenie to zmiana kształtu lub postaci ciała spowodowana działaniem sił zewnętrznych w stosunku do kształtu, wymiaru lub postaci początkowej (odkształcenie inżynierskie) określana bezwymiarowo
Odkształcenie inżynierskie przyjmują postać według wzoru:
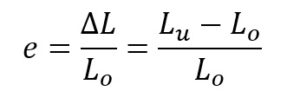
Gdzie:
ΔL– zmiana wymiaru liniowego po lub w trakcie badania
Lo – Wymiar początkowy
Odkształcenie całkowite – jest sumą odkształceń cząstkowych w stosunku do chwilowego wymiaru próbki.
Odkształcenie rzeczywiste zatem przyjmuje postać:
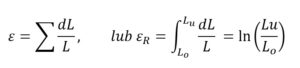
Zazwyczaj L odnosi się do długości odkształcenia liniowego
Dodatkowo istnieje zależność odkształcenia rzeczywistego w przypadku odkształceń złożonych: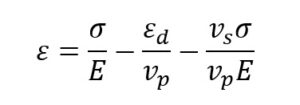
Gdzie:
E – moduł Younga
Vp – współczynnik Poissona w odkształceniach plastycznych
Vs – współczynnik Poissona w odkształceniach statycznych
ε – odkształcenia podłużne rzeczywiste
εd – odkształcenia poprzeczne rzeczywiste
σ – naprężenia powodujące odkształcenie
Współczynnik koncentracji odkształceń
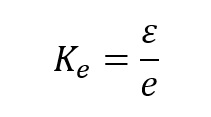
Gdzie
ε – odkształcenia rzeczywiste
e – odkształcenia inżynierskie
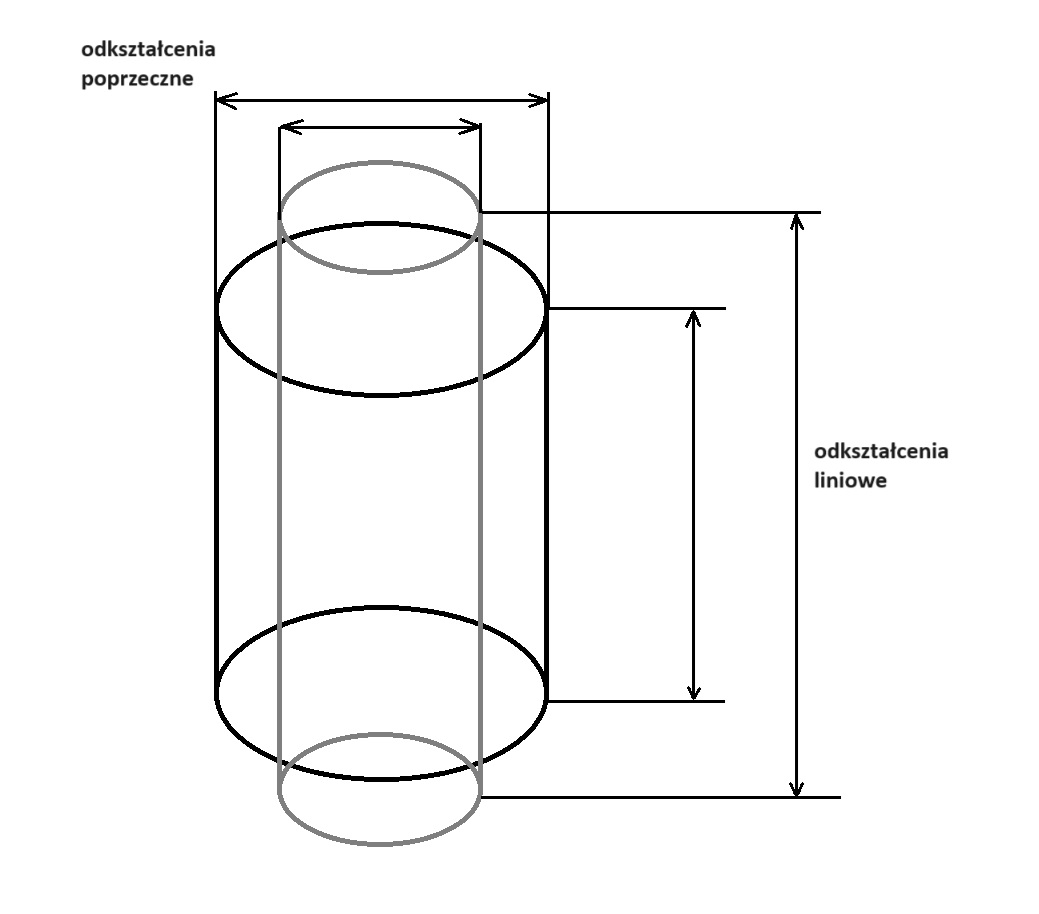
W wąskim zakresie deformacji odkształcenia plastyczne i sprężyste się sumują i występuje zależność:
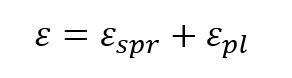
Gdzie:
ε_spr – odkształcenia rzeczywiste w zakresie sprężystym
ε_pl – odkształcenia rzeczywiste w zakresie plastycznym
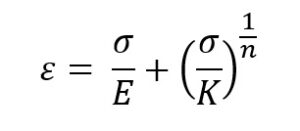
Gdzie:
σ – naprężenia powodujące odkształcenie
K – współczynnik wytrzymałości statycznej
n – wykładnik umocnienia statycznego – opisuje on jak bardzo materiał się umacnia w przypadku przejścia z zakresu sprężystego do zakresu plastycznego (elementy teorii sprężystości)
Odkształcenie obiętościowe
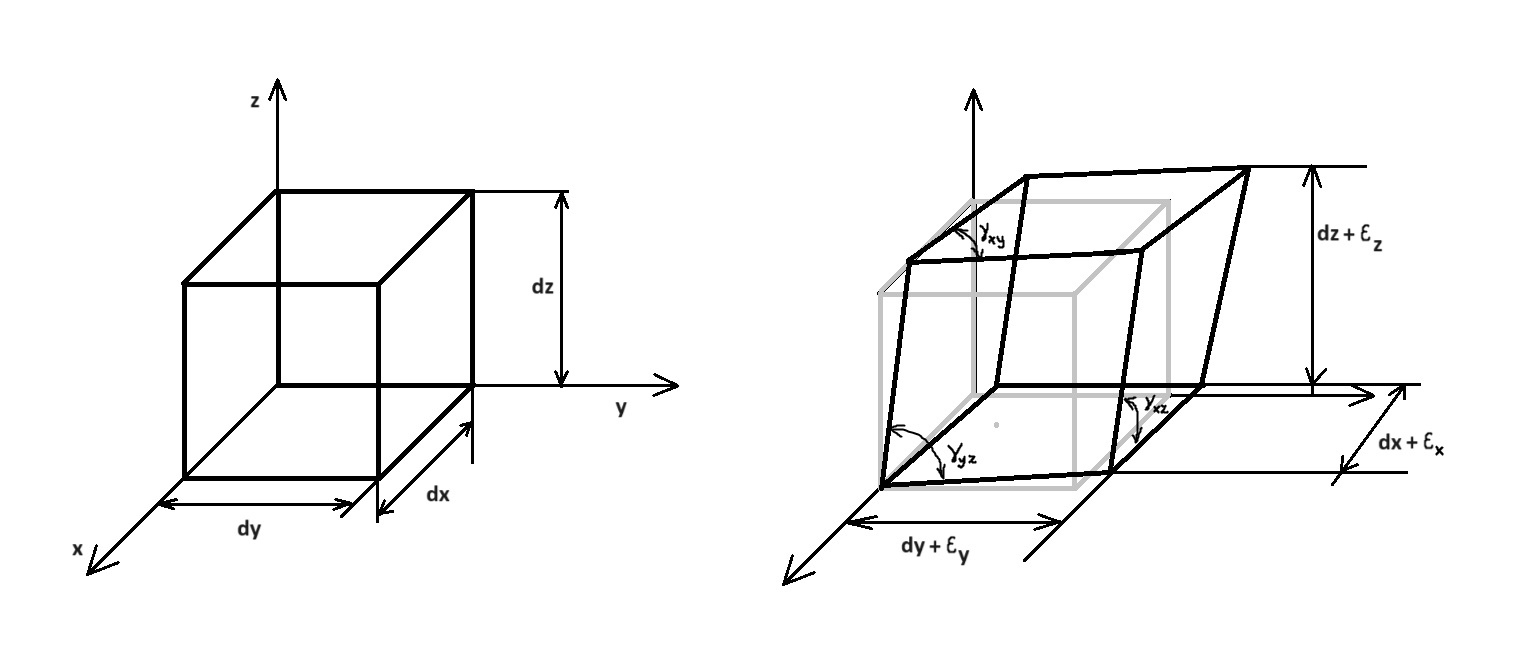
Aby opisać zmianę objętości „elementu” ciała potrzeba jest sześć składowych (3 osie i 3 ustawienia kątowe)
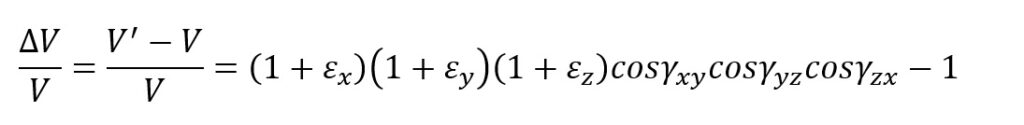
Dla obciążeń wieloosiowych odkształcenia związane z każdym z przyłożonych obciążeń sumują się:
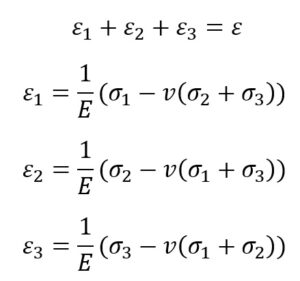
Gdzie :
V – Liczba Poissona
![]()
Spiętrzenie naprężeń
Spiętrzenie naprężeń – to lokalna koncentracja naprężeń materiału na przykład wokół otworu i gwałtownych zmian geometrii
Naprężenia nominalne i maksymalne w przekroju osłabionym
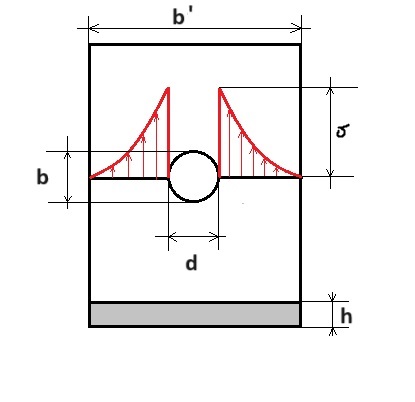
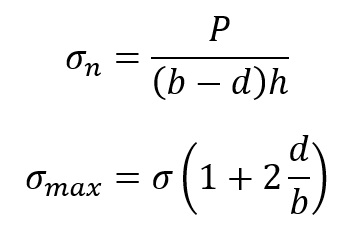
Dla przypadku gdy d=b’![]()
Gdzie
b- średnica (wosokość) otworu
d- średnica(szerokośc) otworu
h- grubość blachy
b’- szerokość blachy
| – współczynnik spiętrzenia naprężeń, można go znaleźć w tablicach, z danych empirycznych dla różnych wymiarów. |
W anglojęzycznej literaturze α oznaczany jest literą k nazywaną współczynnikiem koncentracji naprężeń (stress concentration factor).
Analiza naprężeń i odkształceń
Zaczynając od jednokierunkowego stanu naprężeń jako najprostszy stan
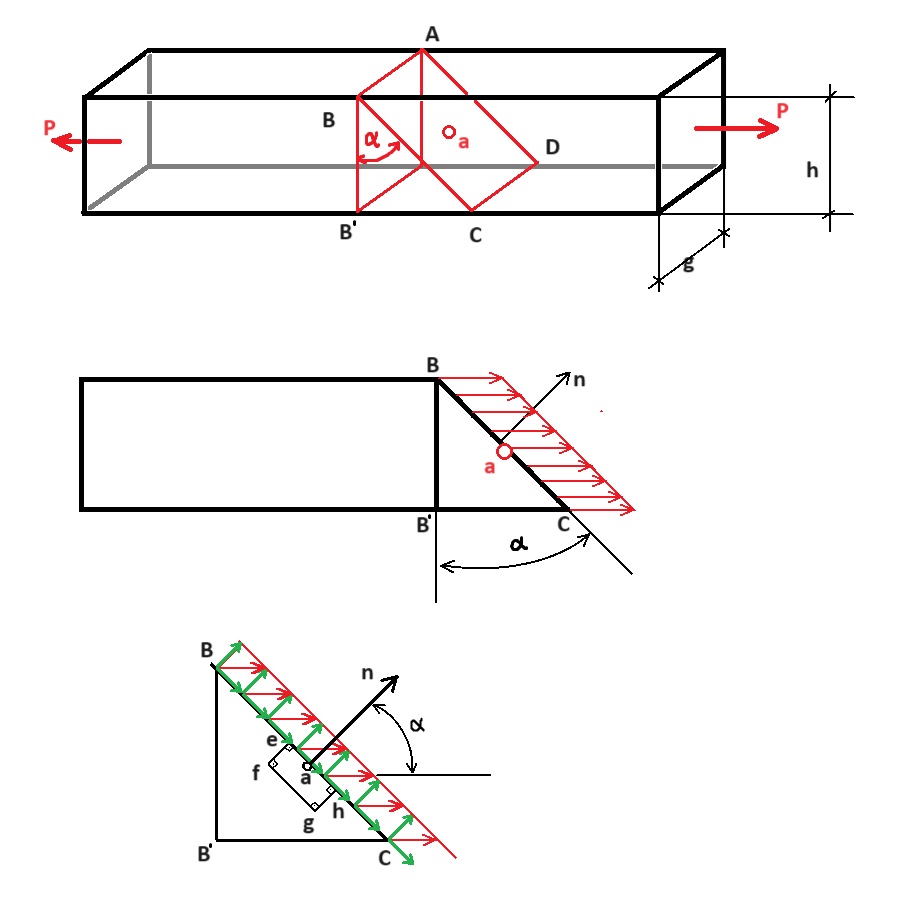
Rozpatrując wycinek efgh jako elementarny, nieskończenie mały
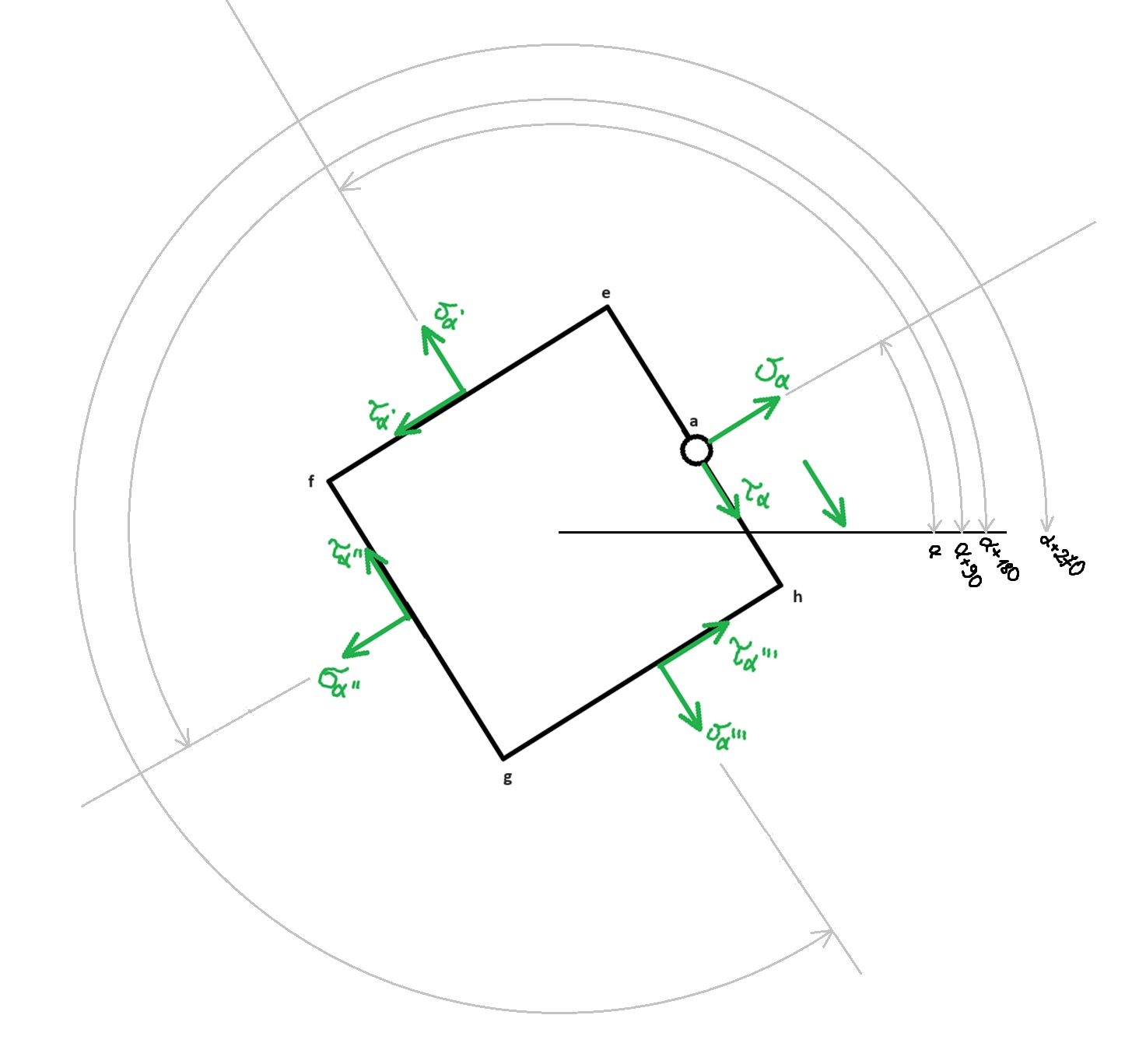
Wyznaczamy wartości naprężeń
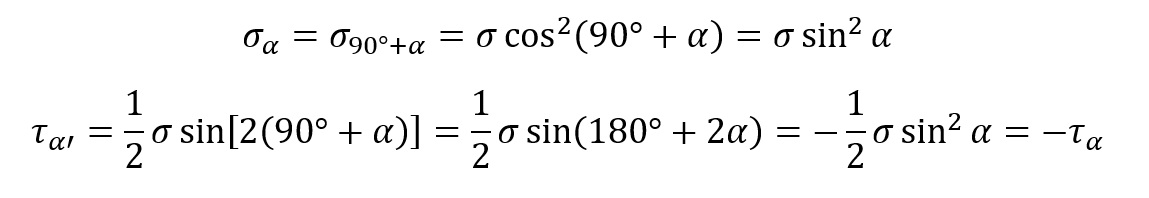
Analogicznie
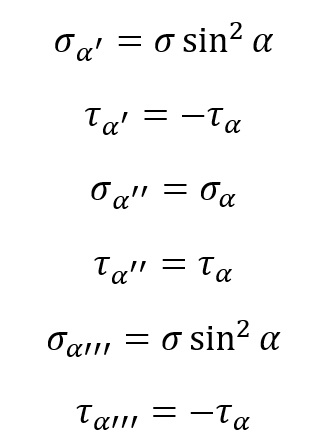
Naprężenia w dwukierunkowym stanie naprężeń, dwukierunkowy (płaski) stan naprężeń
Płaski stan naprężeń to taki który występuje w układach dwuwymiarowych. Ma zastosowanie np. dla przypadku układu płyt cienkich, w których wymiar głębokości (grubości) można pominąć.
Rozpatrzmy płaską blachę:
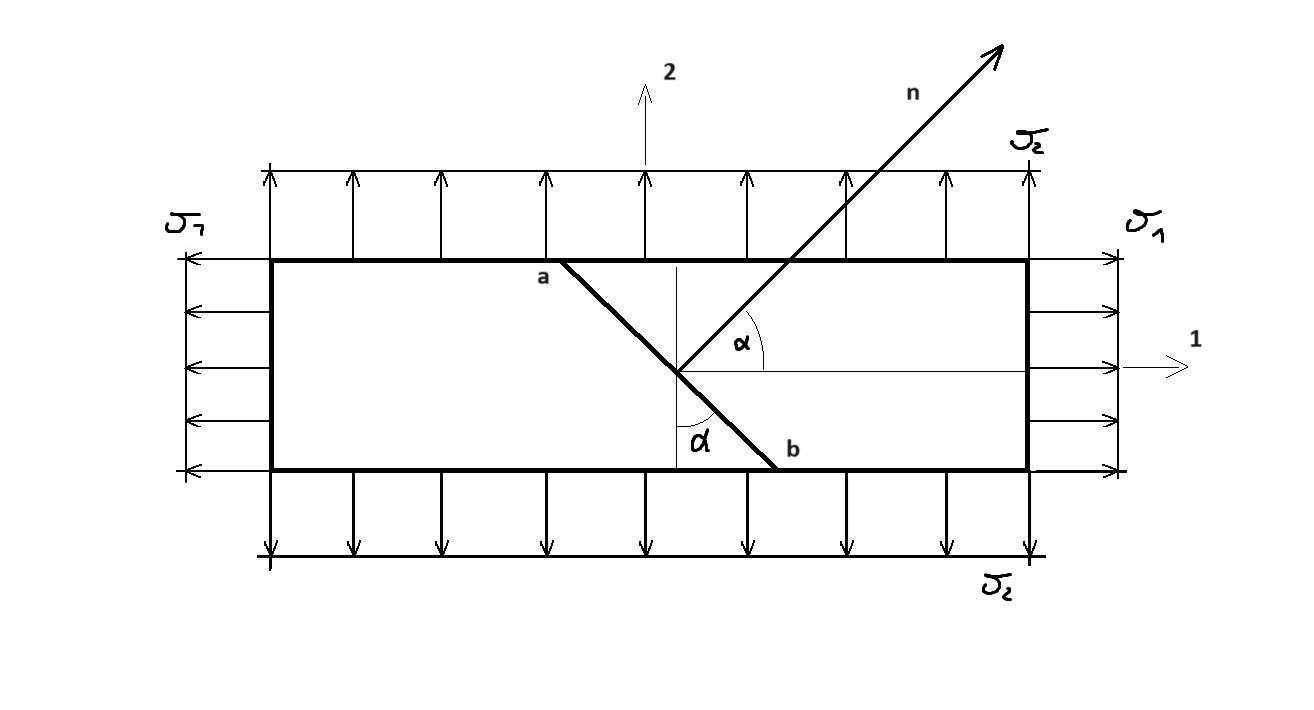
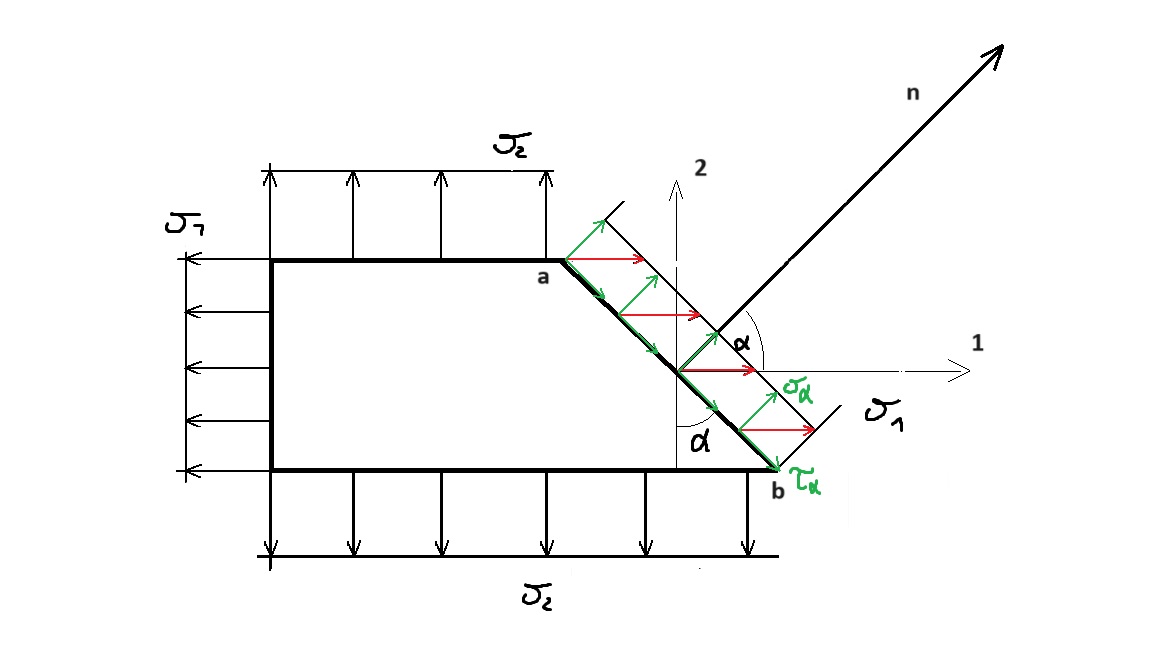
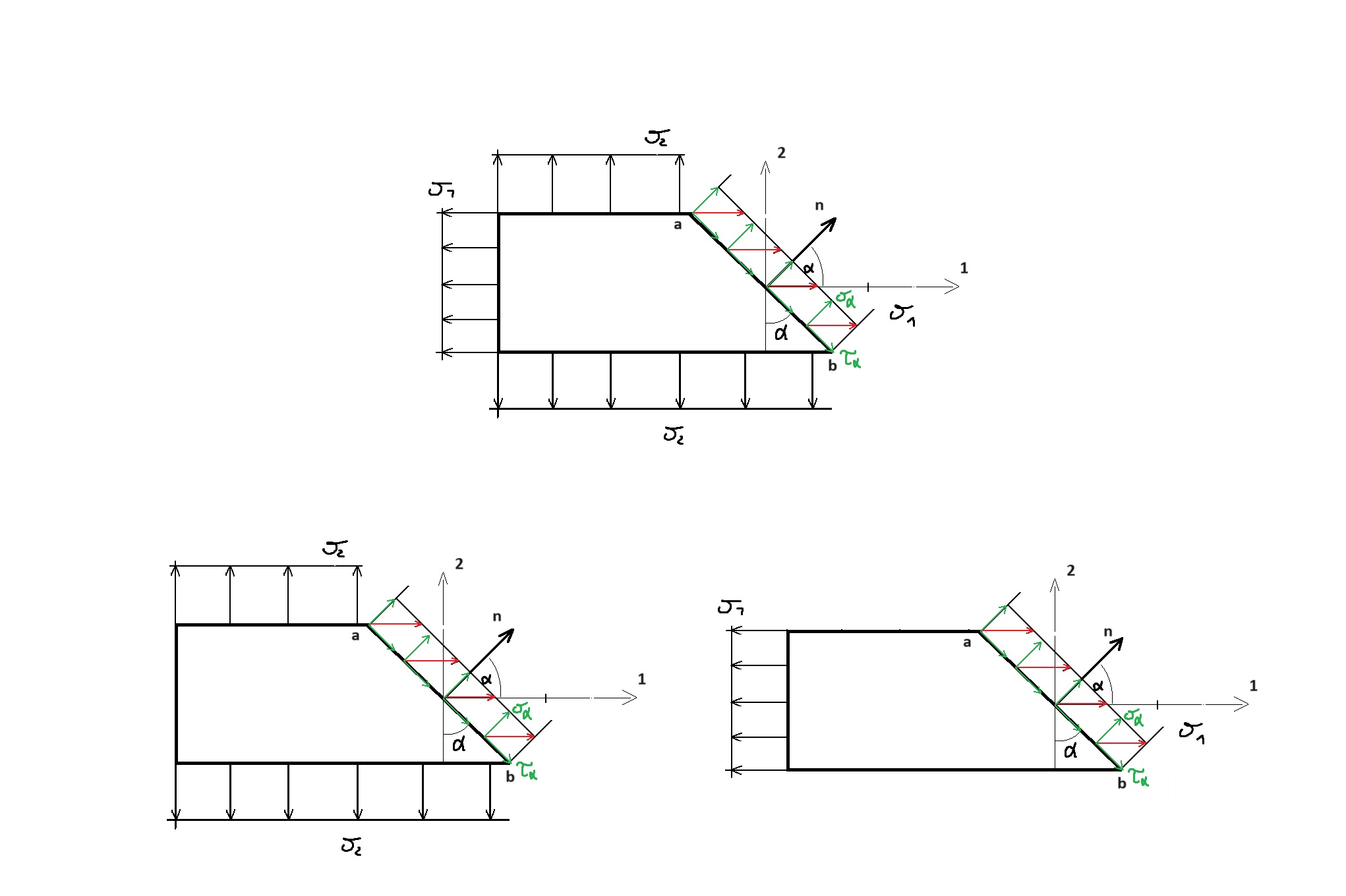
Płaski stan naprężeń można rozważyć jako złożenie (superpozycję) dwóch stanów jednokierunkowych w dwóch osiach.
Gdzie: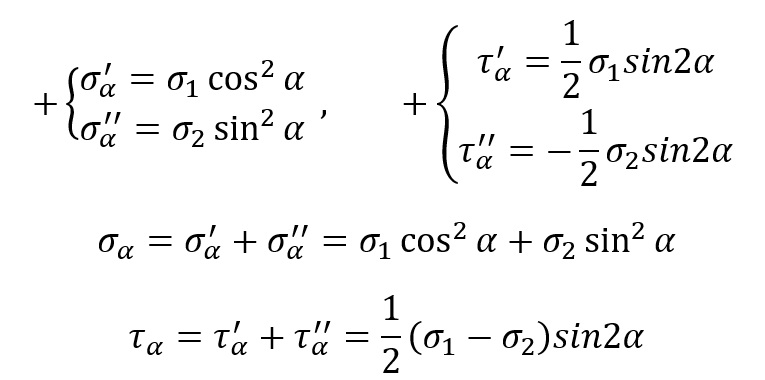
Rysowanie koła Mohra
Koło Mohra – to opracowana przez niemieckiego inżyniera Christiana Mohra metoda graficznej reprezentacji naprężeń dla danych stanów. Przedstawiany jest w prostokątnym układzie współrzędnych σ i τ
Opis metody wykreślnej rysowania koła Mohra
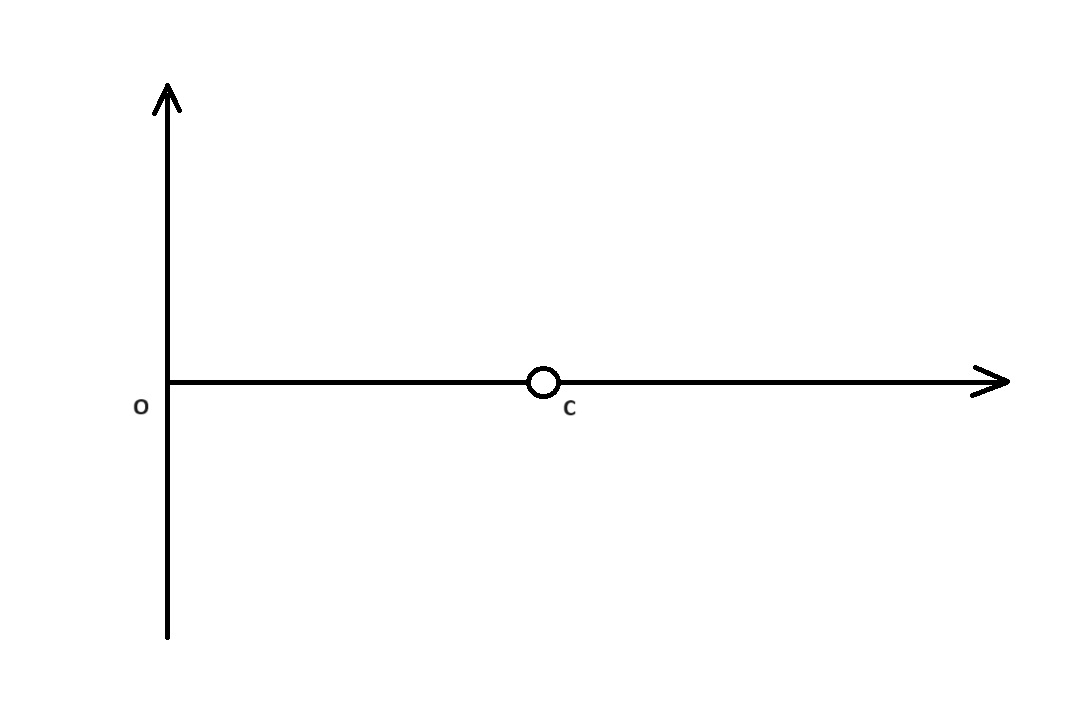
1. Wyznaczamy punkt C – środek koła Mohra, w odległości OC od środka układu współrzędnych
![]() – jest średnią arytmetyczną naprężeń σ 1 i σ 2. Obowiązuje założenie, że σ1 ≥ σ2
– jest średnią arytmetyczną naprężeń σ 1 i σ 2. Obowiązuje założenie, że σ1 ≥ σ2
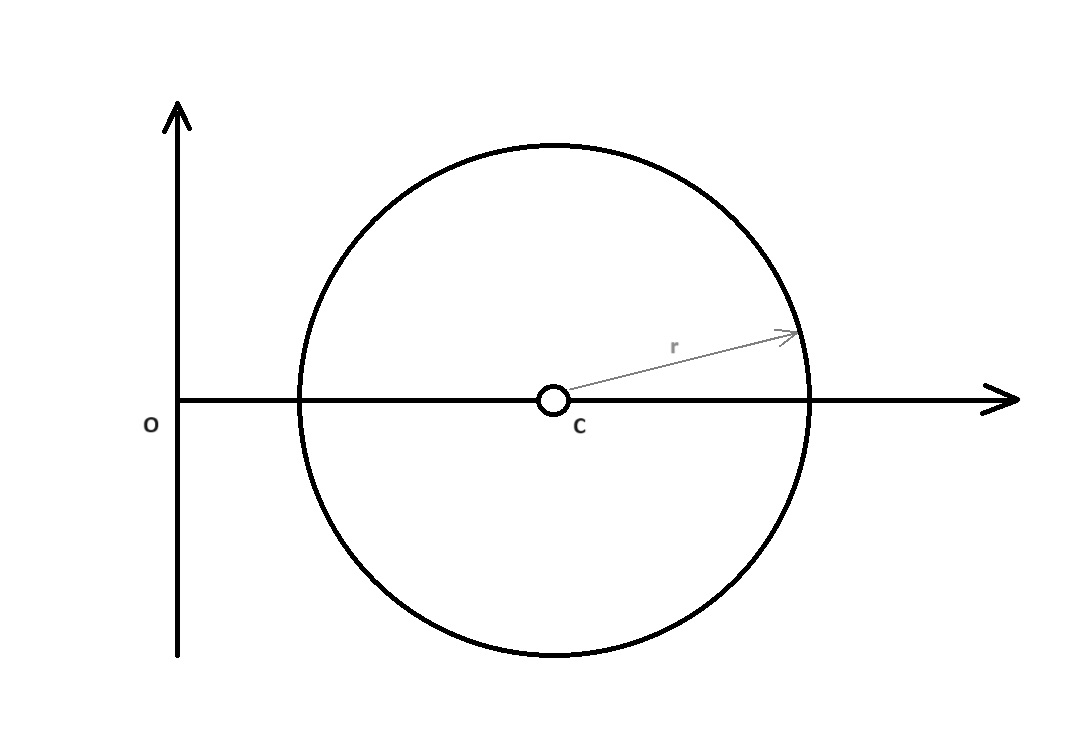
2. Z punktu C zakreślamy koło o promieniu r równemu:![]()
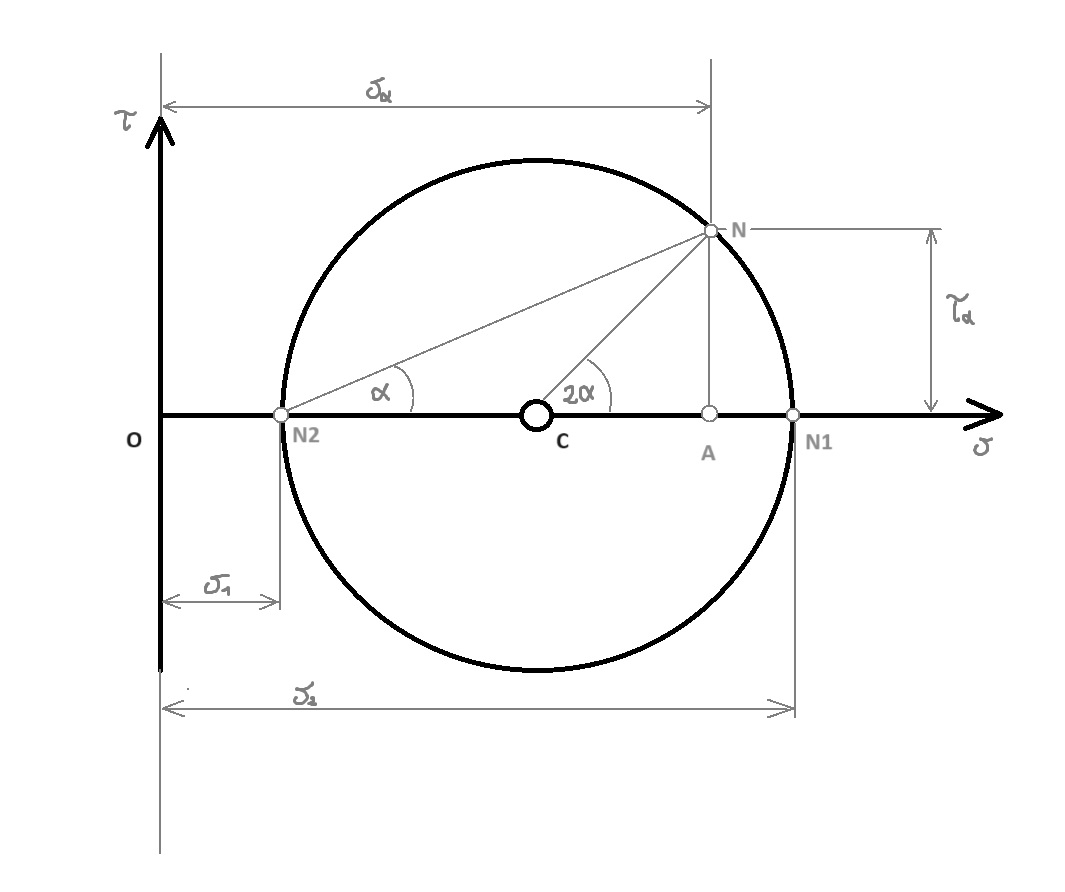
3. Zakreślamy kąt α hipotetyczny, nie jest to żaden konkretny kąt, jest to każdy założony przez nas kąt przekroju.
Punkt N odpowiada przekrojowi A-B blachy. Przekroje w których nie działają naprężenia styczne a jedynie normalne nazywamy przekrojami głównymi i odpowiadają one punktom N1 i N2 na rysunku. Odmierzane zgodnie z konwencją, czyli z kierunkiem wskazówek zegara od punktu N1 wokół punktu C.
Koło Mohra dla układu przestrzennego
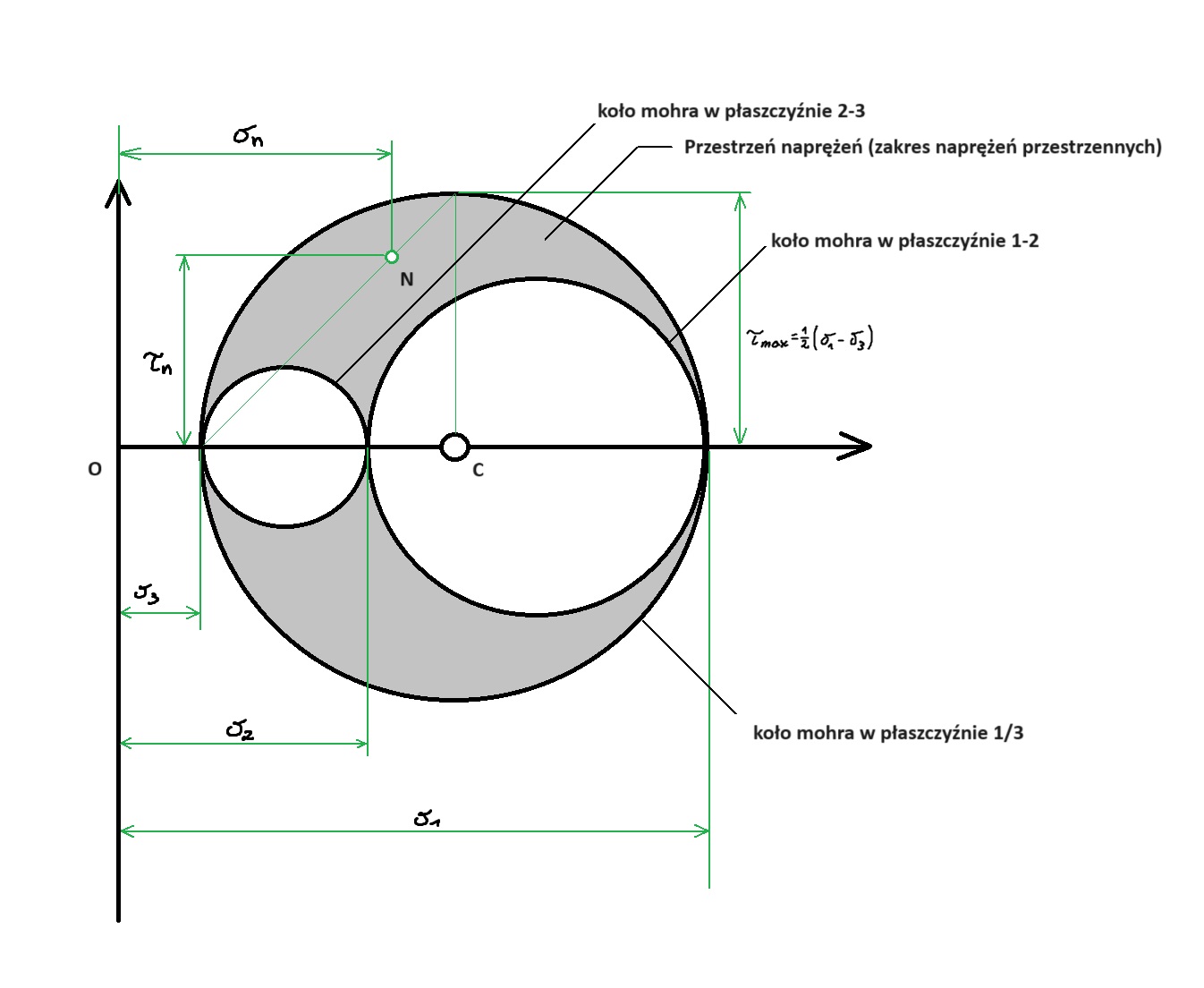
Przestrzenny układ naprężeń
Rozpatrzmy sześcienną kostkę reprezentującą przestrzenny stan naprężeń:
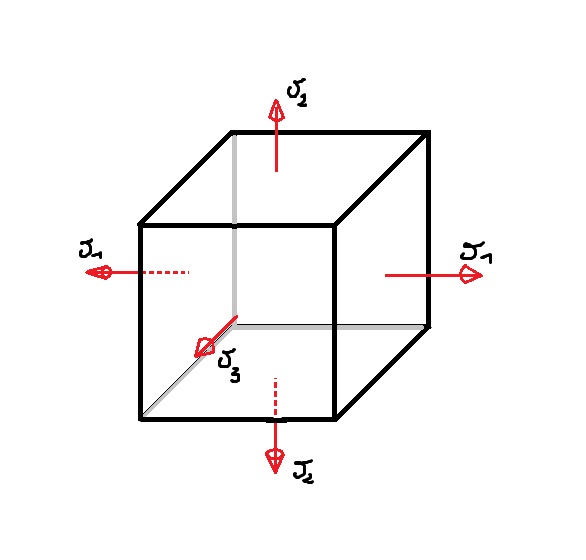
Zakładając, że σ1 ≥σ2 ≥ σ3 oraz uwzględniając naprężenia na kostce w układzie kartezjańskim