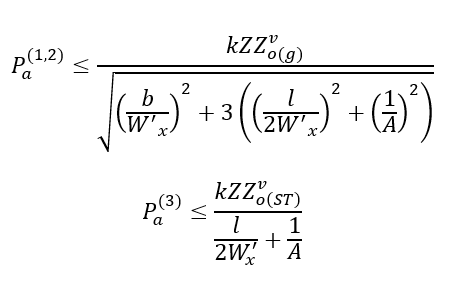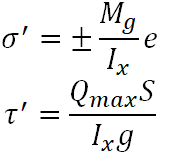Obliczenia połączeń spawanych
Spis treści
Projektowanie połączeń spawanych – rozkład naprężeń
Obliczanie połączenia spawanego
-
Naprężenia dopuszczalne połączenia spawanego dla spoiny czołowej
-
Naprężenia dopuszczalne połączenia spawanego dla spoin pachwinowych – obliczanie spoiny pachwinowej połączenia spawanego
-
Obliczanie wysokości spoiny pachwinowej – minimalna grubość spoiny pachwinowej
-
Naprężenia dopuszczalne połączenia spawanego – wzór ogólny
Warunki wytrzymałości spoin przy obciążeniach prostych
Tabela warunków wytrzymałościowych spoin
przy obciążeniach złożonych
Przykład obliczeniowy połączenia spawanego
Obliczenia Spoiny Skręcanej i Zginanej
Obliczenia połączeń spawanych to proces projektowania i analizy spoin pod kątem ich wytrzymałości i bezpieczeństwa. Uwzględnia obciążenia, materiał oraz warunki pracy, by zapewnić trwałość i niezawodność. Aby zacząć budować model obliczeniowy połączenia spawanego należy dokładnie wiedzieć, jak zachodzi proces spawania różnymi metodami. Dzięki temu będziemy wiedzieć o stosowalności naszych obliczeń oraz granicach, o których musimy pamiętać.
Przy łączeniu materiału ze sobą, za pomocą spawania w miejscu spoiny aby wytopić materiał zazwyczaj wprowadzamy dużą ilość ciepła. To ciepło sprawia, że metal w obszarze spawania rozszerza się, a kiedy później się ochładza, próbuje skurczyć się z powrotem. Problem polega na tym, że metal nie może się swobodnie skurczyć z powodu swojej sztywności i obecności chłodniejszych obszarów dookoła spoiny. To prowadzi do „zamknięcia” w metalu pewnych napięć, podobnie jak sprężyny, które zostały naciągnięte lub ściśnięte i nie mogą wrócić do swojego pierwotnego stanu. Dla obliczeń analitycznych projektowania połączenia spawanego – przedstawionych poniżej, efekt ten się pomija. Jednak należy o nim pamiętać. Natomiast sama geometria spoiny, będąca wynikiem procesu spawania (dokładania materiału) wpływa na przebieg naprężeń w materiale. Ten efekt nazywamy spiętrzeniem naprężeń. Zgodnie z analogią hydrodynamiczną naprężeń, przepływają one jak woda w rzece będąc zaburzonymi w miejscu spoiny, piętrząc się.
W celu niwelowania naprężeń spawalniczych w niektórych przypadkach ogrzewa się materiał do pewnej temperatury i powoli wychładza.
Poniżej przedstawione zostały prawdopodobne przebiegi linii sił i rozkład naprężeń normalnych.
Rozkład naprężeń w przekroju spoiny czołowej
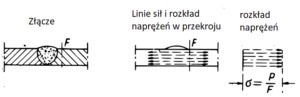
W spoinie czołowej, naprężenia przepływają z pominięciem wypustu, najważniejsze aby spoina nie miała wgłębień, ponieważ we wgłębieniach następuje spiętrzenie.
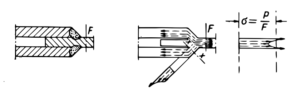
Rozkład naprężeń w przekroju spoiny połączenia nakładkowego
Rozkład naprężeń w przekroju spoiny połączenia zakładkowego
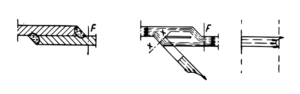
Rozkład naprężeń w przekroju dwustronnej spoiny pachwinowej
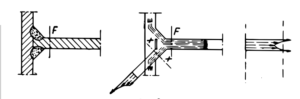
Rozkład naprężeń w przekroju jednostronnej spoiny pachwinowej
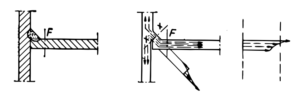
Rozkład naprężeń w przekroju spoiny typu K
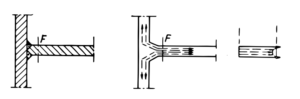
Obliczenia połączeń spawanych – metodyka
Dla obliczenia połączeń spawanych najlepszą hipotezą wytrzymałościową stanowi hipoteza Hubera–von Misesa, która zakłada, że zniszczenie materiału następuje, gdy energia odkształcenia postaciowego osiągnie wartość graniczną. Hipoteza ta sprawdza się szczególnie dobrze w spawanych konstrukcjach, ponieważ uwzględnia wpływ naprężeń w różnych kierunkach, co pozwala na precyzyjniejsze oszacowanie stanu granicznego materiału.
Obliczenia połączeń spawanych obejmują głównie dwa rodzaje spoin: spoiny czołowe i spoiny pachwinowe. Spoina czołowa, stosowana przy łączeniu elementów o równej grubości, charakteryzuje się pełnym przetopem i wysoką wytrzymałością na rozciąganie. Z kolei spoina pachwinowa, używana do łączenia elementów pod kątem względem siebie, wymaga analizy ścinania, które jest kluczowe dla oceny jej wytrzymałości.
Proces obliczeń uwzględnia:
- Rodzaj materiału – uwzględniający jego właściwości mechaniczne, takie jak granica plastyczności i wytrzymałość na pękanie.
- Naprężenia– analizowane pod kątem rozciągania, ścinania i skręcania.
- Współczynniki bezpieczeństwa – zapewniające margines wytrzymałości konstrukcji w ekstremalnych warunkach.
- Grubość spoiny – odpowiednio dobrana, aby zapewnić nośność zgodnie z normami
Więcej szczegółowych informacji na ten temat można znaleźć w naszym artykule o wytrzymałości materiałów, gdzie opisano podstawy teoretyczne i praktyczne zastosowania tej hipotezy.
Naprężenia dopuszczalne połączenia spawanego dla spoiny czołowej
W spoinie czołowej obciążenia są analizowane zgodnie z ich rzeczywistym charakterem, a to oznacza, że:
- Naprężenia normalne (σ) wynikające z obciążeń prostopadłych do przekroju spoiny traktujemy jako naprężenia normalne.
- Naprężenia styczne (τ) wynikające z obciążeń równoległych do przekroju spoiny traktujemy jako naprężenia styczne.
Jest to istotne w kontekście analizy wytrzymałości, ponieważ
Naprężenia zastępcze więc przyjmują postać :
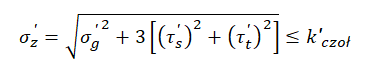
W przypadku znacznej dominacji naprężeń stycznych (np. dla spoiny skręcanej) – naprężenia zastępcze mają charakter naprężeń ścinających a więc stycznych co jest zgodne z poniższym:
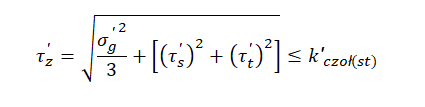
Gdzie :
„‘ ” oznacza naprężenia występujące w spoinie, nie w materiale rodzimym

Naprężenia dopuszczalne połączenia spawanego dla spoin pachwinowych – obliczanie spoiny pachwinowej
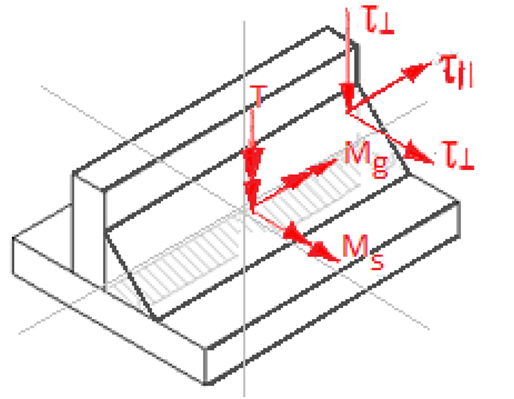
W przypadku spoin pachwinowych zmienia się podejście do traktowania naprężeń. W spoinach pachwinowych zarówno naprężenia normalne (σ) występujące w przekroju spoiny, jak i naprężenia styczne (τ) są traktowane jako naprężenia styczne. Oznacza to, że w tych spoinach uwzględnia się tylko efekt ścinania w analizie naprężeń.
- Naprężenia teoretycznie normalne (σ) wynikające z obciążeń prostopadłych do przekroju spoiny traktujemy jako naprężenia styczne.
- Naprężenia styczne (τ) wynikające z obciążeń równoległych do przekroju spoiny traktujemy jako naprężenia styczne.
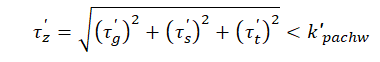
Z racji tego, że traktujemy wszystkie naprężenia jak naprężenia styczne to dodajemy je zgodnie z zasadą dodawania wektorów.
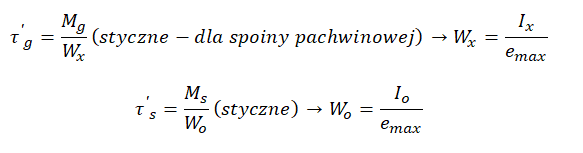
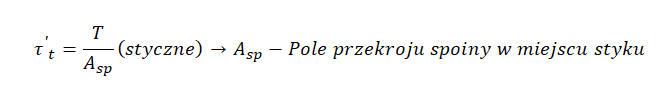
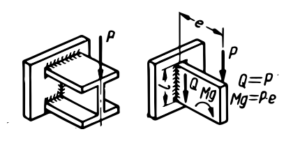
Dla spoiny dwustronnej skręcanej pachwinowej :
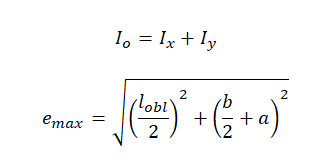
Obliczanie wysokości spoiny pachwinowej – minimalna grubość spoiny pachwinowej
W przypadku spawania nie zawsze elementy są tej samej długości i grubości. Z tego względu możemy wyróżnić dwa przypadki dla których należy dobrać odpowiednią grubość spoiny
Pierwszy, w którym grubość blachy dospawanej prostopadle jest większa niż grubość blachy podstawy – minimalna grubość spoiny pachwinowej wynosi:
Drugi w którym grubość blachy dospawanej prostopadle jest mniejsza niż grubość blachy podstawy – minimalna grubość spoiny pachwinowej wynosi :
Naprężenia dopuszczalne połączenia spawanego – wzór ogólny
Naprężenia dopuszczalne połączenia spawanego to maksymalne wartości naprężeń, jakie materiał spoiny może wytrzymać bez ryzyka uszkodzenia. Ich określenie jest niezbędne podczas obliczania połączeń spawanych i projektowania połączenia spawanego, aby zapewnić bezpieczeństwo konstrukcji. W ramach obliczeń wytrzymałościowych połączeń spawanych bierze się pod uwagę takie czynniki jak warunki eksploatacji, rodzaj obciążenia (statyczne lub dynamiczne) oraz potencjalne skutki zmęczenia materiału.
Dla obciążeń statycznych zakłada się że naprężenia dopuszczalne połączenia spawanego przyjmują postać :
k’– naprężenia dopuszczalne dla spoiny
z– współczynnik jakości spoiny
=0,5 – przyjmujemy dla spoiny zwykłej jakości (oznacza to, że dopuszczamy dwukrotne osłabienie spoiny z samego faktu braku kontroli jej jakości)
=1 – przyjmujemy dla spoiny kontrolowanej
zo – współczynnik rodzaju obciążenia
Poniżej przedstawione są wartości współczynnika rodzaju obciążenia dla danego rodzaju obciążenia
| Rodzaj spoiny | Rodzaj obciążenia statycznego | Zo |
| Czołowe | ||
| Sciskanie | 0,85 | |
| Zginanie | 0,80 | |
| Rozciąganie | 0,75 | |
| Styczne | 0,65 | |
| Pachwinowe | ||
| wszystkie | 0,65 |
Dla spoin pachwinowych wszystkie naprężenia przenoszone są jako naprężenia styczne. Dzięki temu łatwiej zapamiętać, że wszystkie obciążenia mają taki sam współczynnik rodzaju obciążenia dla tych spoin.
k – naprężenia dopuszczalne dla materiału rodzimego
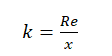
Re– granica plastyczności materiału
x– współczynnik bezpieczeństwa
Dla obciążeń dynamicznych istnieje specjalny współczynnik obliczeniowy dla spoin Za, natomiast wzór na naprężenia dopuszczalne dla spoiny przyjmuje postać
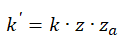
Za –współczynnik rodzaju obciążeń i kształtu dla spoiny przy obciążeniach dynamicznych
Warunki wytrzymałości spoin przy obciążeniach prostych
| Rodzaj obciążenia | Schemat obciążenia | Przekrój obliczeniowy | Warunek wytrzymałościowy |
| Roziąganie |  |
 |
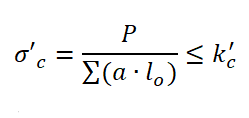 |
| Ścinanie | 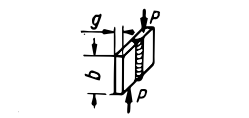 |
 |
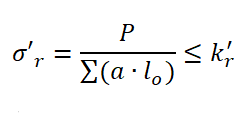 |
| Ścinanie | 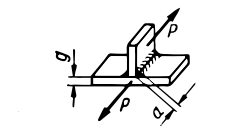 |
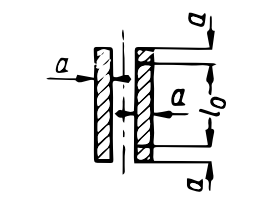 |
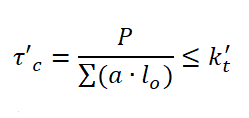 |
| Ścinanie | 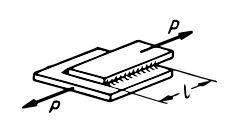 |
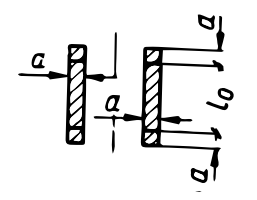 |
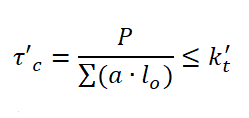 |
| Ścinanie | 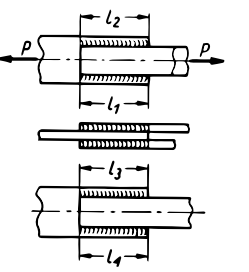 |
 |
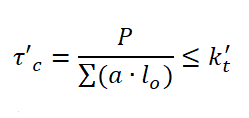 |
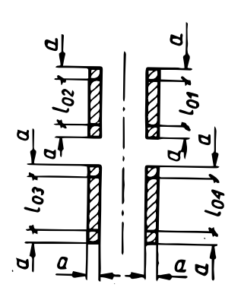
| Ścinanie | 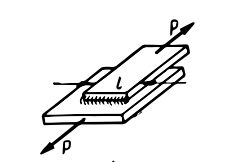 |
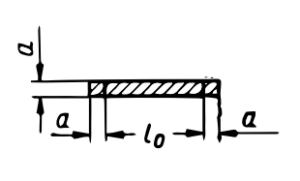 |
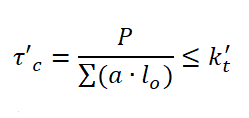 |
| Ścinanie |  |
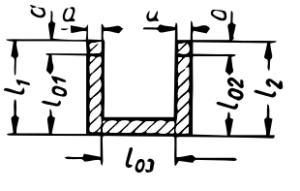 |
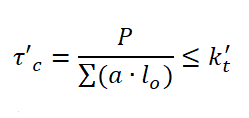 |
Tabela warunków wytrzymałościowych spoin dla obciążeń złożonych
Aby uprościć obliczanie spoin można skorzystać z przedstawionej poniżej tabeli. Zawiera ona gotowe wzory na naprężenia zredukowane i geometrie spoin.
| Połączenie | Przekrój obliczeniowy | Naprężenia obliczeniowe | Naprężenia zredukowane |
|
Połączenie w belkach zginanych
|
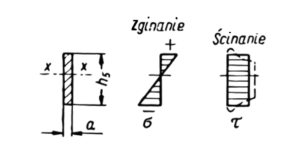 |
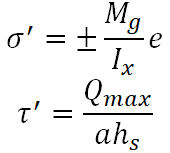 |
|
|
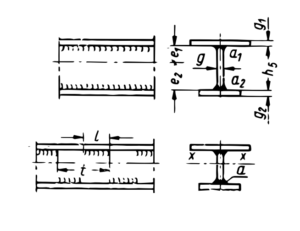
Spoina wzdłużna w belkach zginanych obciążonych momentem Mg i siłą poprzeczną Q
|
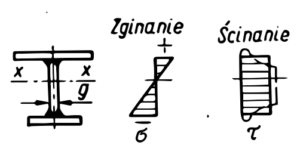 |
Dla spoiny przerywanej
g=2a – dla spoiny dwustronnej pachwinowej S- moment statyczny względem centralnej osi bezwładności x, części przekroju poprzecznego
|
|
|
Spoina pachwinowa obciążona momentem gnącym Mg i siłą poprzeczną Q
|
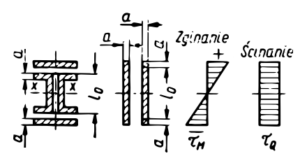 |
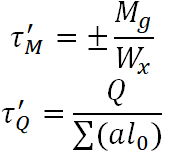 |
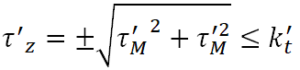 |
|
Spoina pachwinowa obciążona momentem skręcającym, momentem gnącym i siłą poprzeczną
|
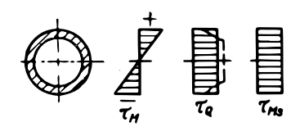 |
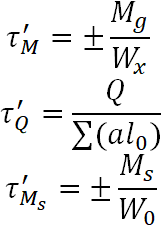 |
Przykład obliczeniowy połączenia spawanego
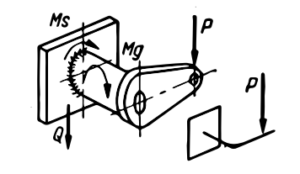
Aby najlepiej zrozumieć proces obliczeniowy przedstawiamy poniżej idealny przykład obliczania wytrzymałości połączeń spawanych wspornika wykonanego ze stali.
Treść : Wspornik traktowany jako metalowa konstrukcja spawana, obciążony został dwiema składowymi siłami P. Należy sprawdzić jego bezpieczeństwo.
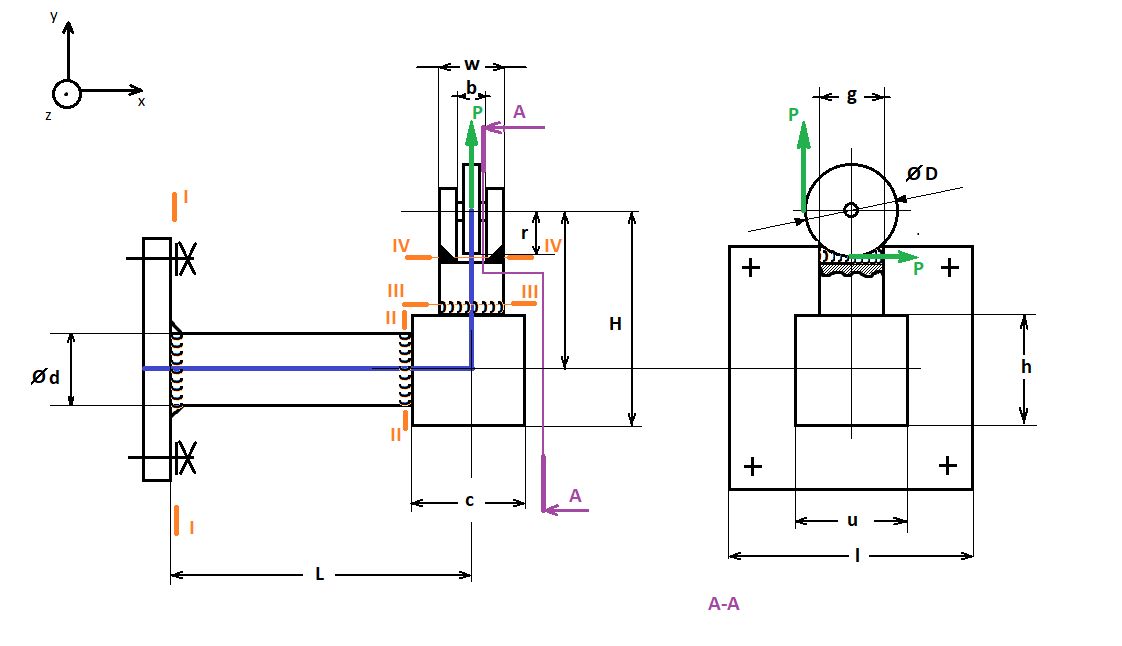
Dane:
d, b, D, n, c, u, h, r, H, Re, X, z, z_a, Zog, Zor, Zoc, Zost
Re-440MPa – granica plastyczności
Rm = 600MPa – granica wytrzymałości materiału na rozciąganie
μ = 0 – wzpółczynnik tarcia
X=2,5 – współczynnik bezpieczeństwa
Wprowadzamy model uproszczony
Na początku należy wprowadzić uproszczony model belkowy układu. Wprowadzenie takiego modelu pozwala nam na oszczędzanie informacji do takich, które są przydatne w danym momencie.
Na pierwszym rysunku oznaczone zostały miejsca niebezpieczne symbolami I,II,III i IV. Takie niebezpieczne miejsca wyznaczamy sami na podstawie modelu obciążeń, tam gdzie pojawią się największe obciążenia na konstrukcji i tam gdzie spodziewamy się spiętrzeń naprężeń. W przypadku liczenia połączeń spawanych przekrojem niebezpiecznym jest przekrój występowania spoiny – ponieważ ją chcemy liczyć i zakładamy, że to ona jest niebezpieczna. Jako pierwsze, należy wyznaczyć ogólny rozkład sił na wsporniku. Pomijamy geometrię i na potrzeby „abstrakcyjnych” obliczeń zakładamy wszystkie elementy konstrukcyjne jako liniowe. Na tym etapie jeszcze nie liczymy docelowych spoin a jedynie rozkładamy obciążenia, które będą nam uszkadzać spoiny w konkretnych miejscach.
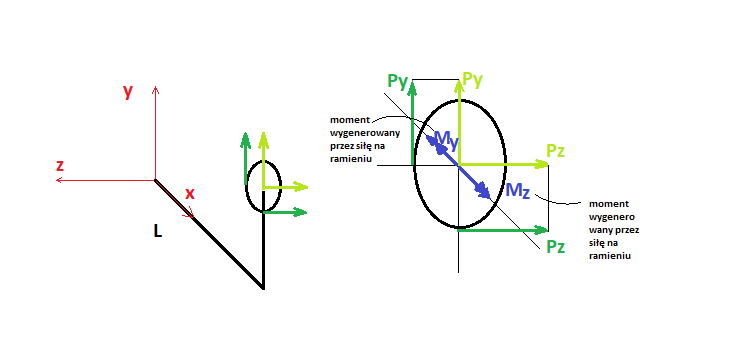
Wprowadzamy globalny układ współrzędnych i przeprowadzamy obliczenia sił i momentów działających na wspornik
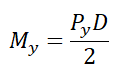
My – to moment w osi Y od siły Py
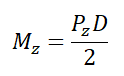
Mz – to moment w osi Z od siły Pz
Następnym krokiem jest naniesienie rozkładów sił i momentów na uproszczonym modelu belkowym.
Długie ramie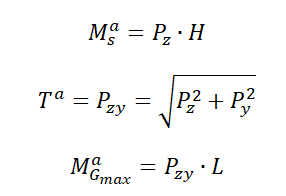
Ms – moment skręcający ramię
Ta – siła tnąca działająca na ramię
MG_max – maksymalny moment gnący
Krótkie ramie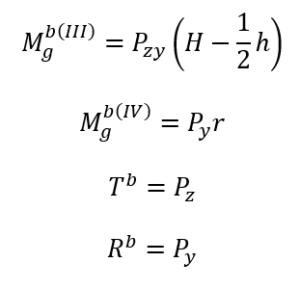
Krótkie ramie jak widzimy z modelu jest dodatkowo rozciągane składową Py
Na podstawie rozkładów sił, oraz geometrii należy wyznaczyć przekroje z uwzględnieniem miejsc spoin
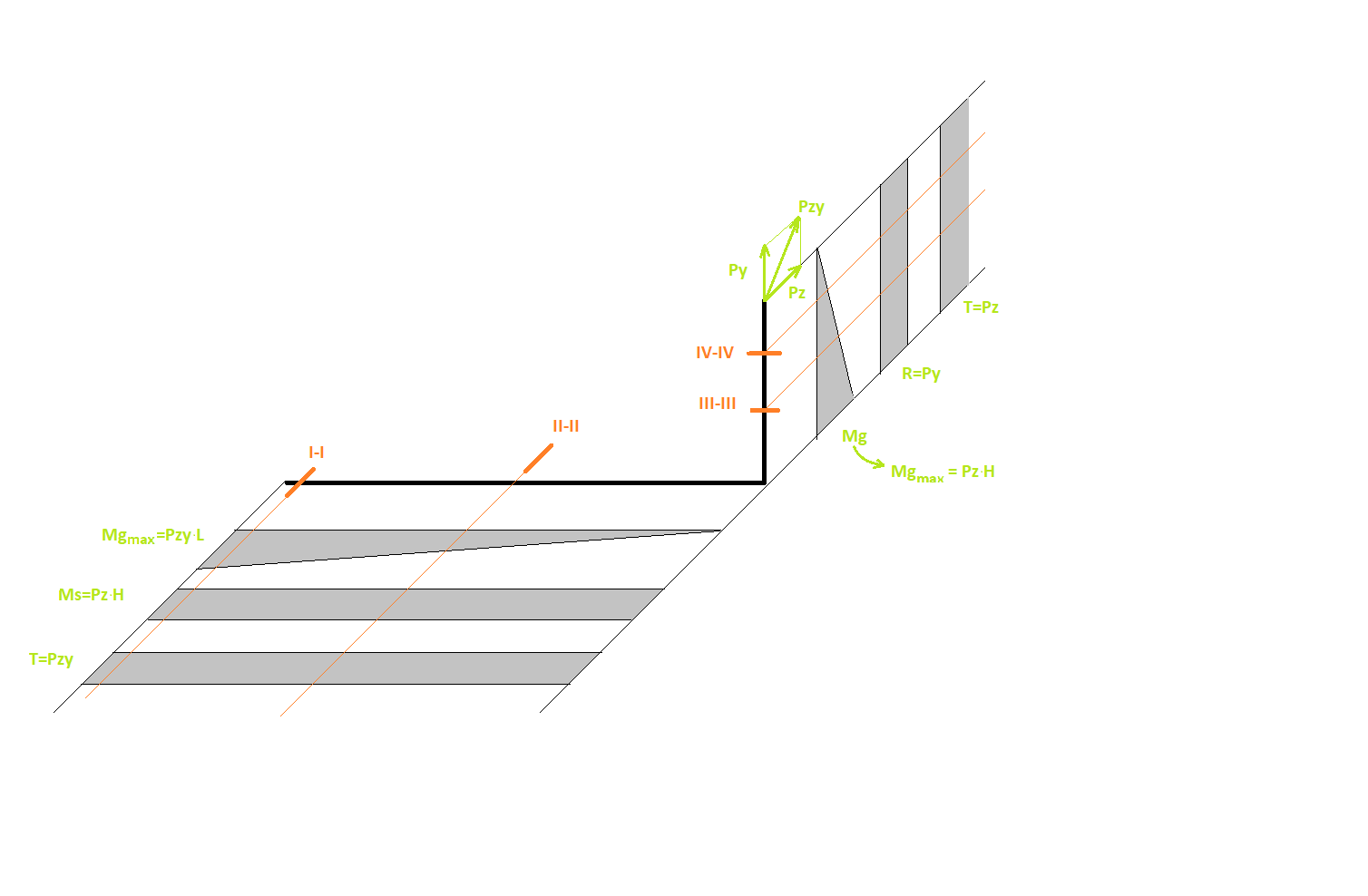
Obliczanie Przekrojów niebezpiecznych spoiny
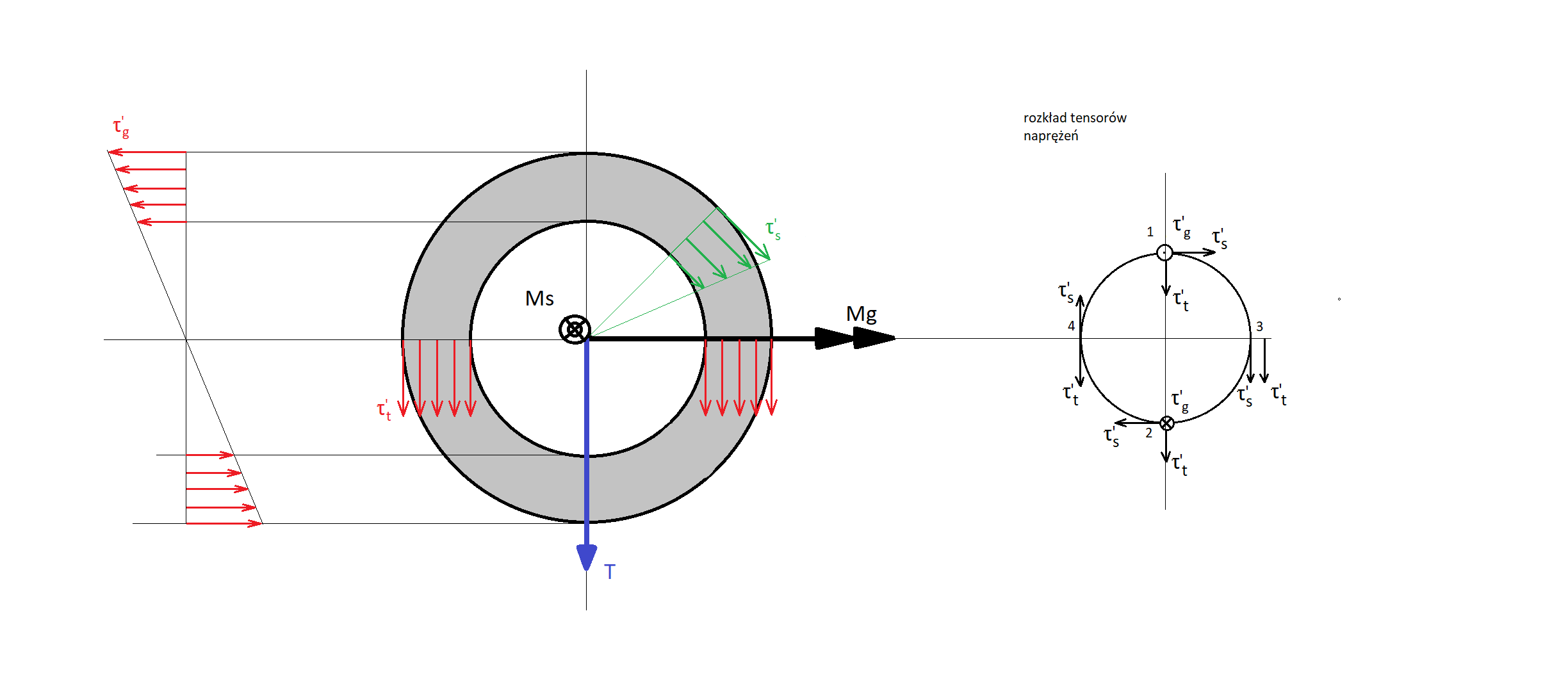
Przekrój I-I
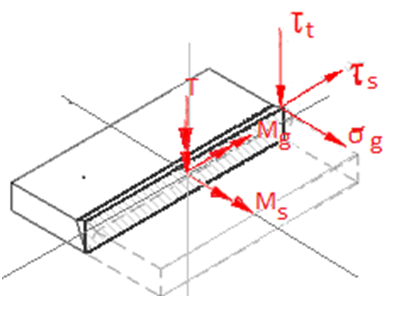
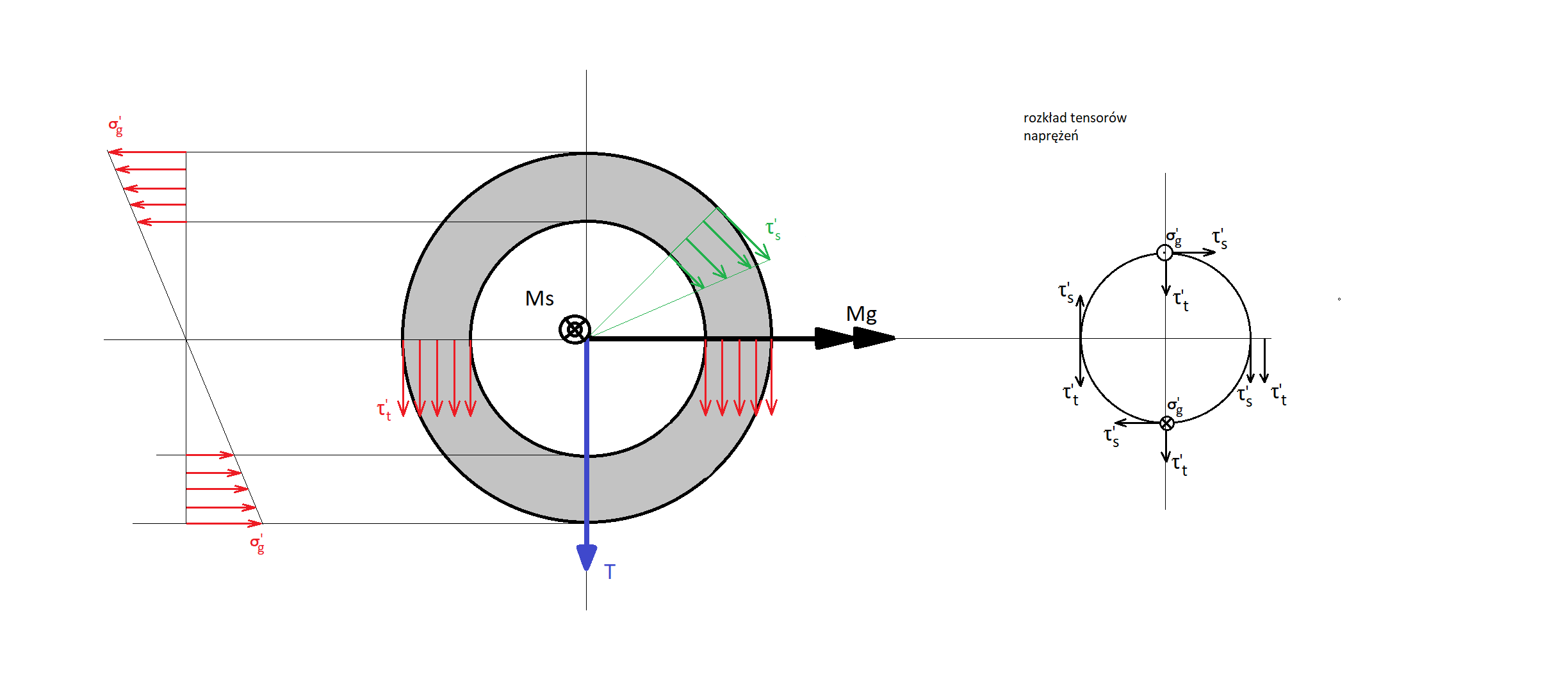
Rysunek miejsca przekroju w miejscu I-I. Należy zwrócić uwagę na położenie przekroju względem globalnego układu współrzędnych oraz nanieść na niego obciążenia zgodnie z kierunkami według modelu uproszczonego. Obok rysunku przedstawiającego przekrój spoiny przedstawiony jest inny rysunek zawierający nałożenie tensorów naprężeń na geometrię spoiny i wyznaczenie konkretnego punktu w którym będziemy liczyć wpływ tych tensorów naprężeń na naprężenie zastępcze w tym miejscu. Naprężenie zastępcze to naprężenie zgodnie z hipotezą Hubera – Von Missesa
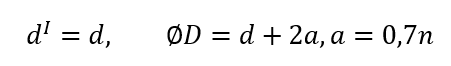
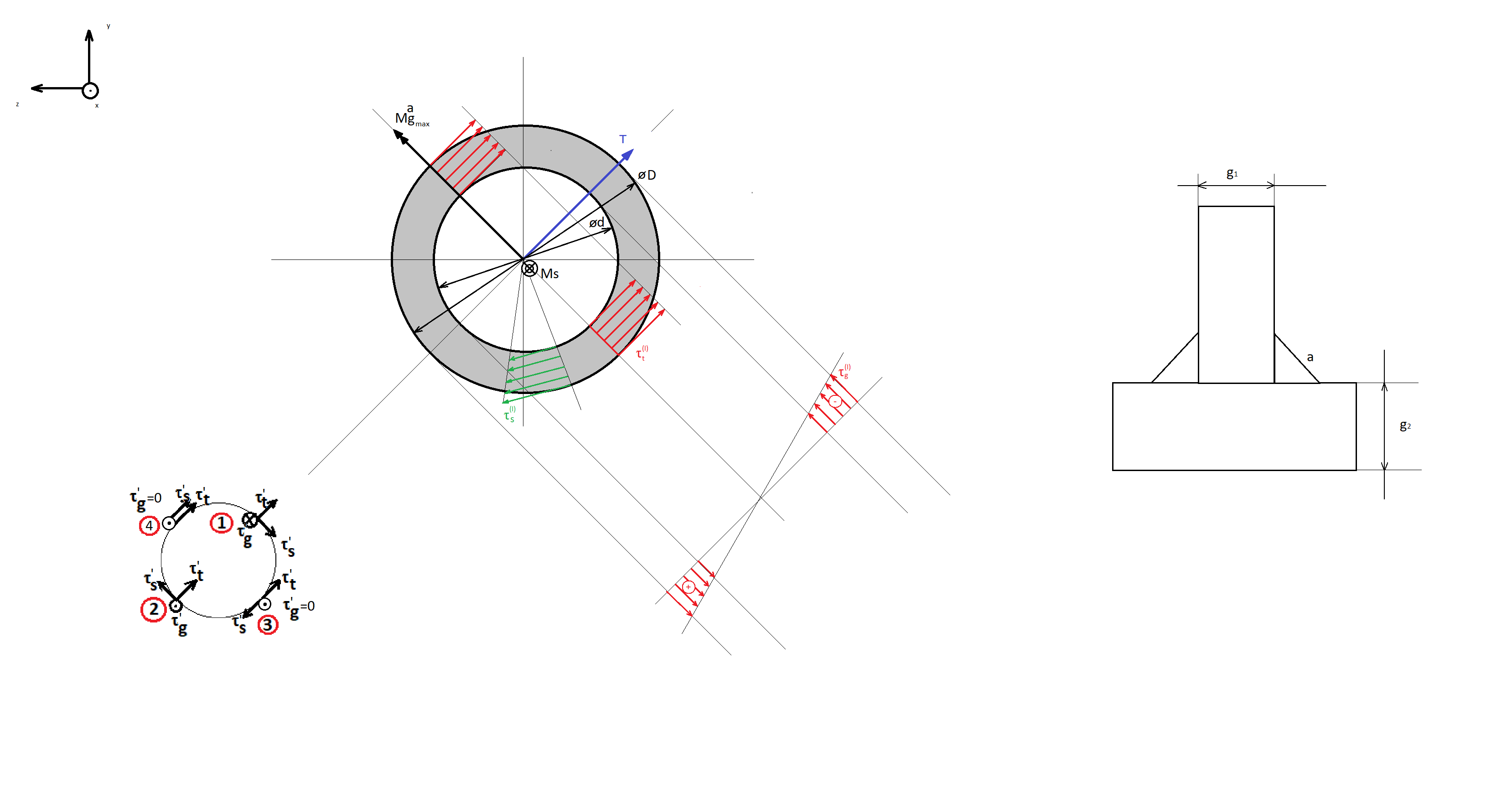
Wzory naprężeń i naprężeń zastępczych dla punktów najbardziej obciążonych, zgodnie z rysunkiem powyżej
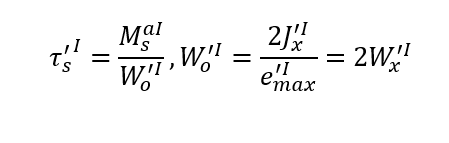
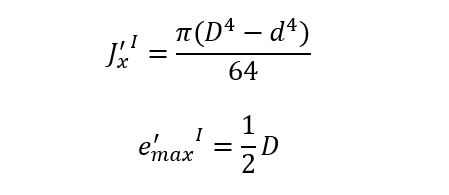

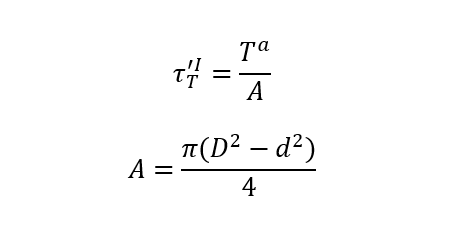
gdzie
Jx – moment bezwładności względem wprowadzonej osi obojętnej zginania x
Jo = 2Jx biegunowy moment bezwładności – suma momentów osiowych względem
prostopadłych osi przechodzących przez ten biegun.
Wx – wskaźnik wytrzymałości przekroju (na zginanie) w osi x. Wskaźniki wytrzymałości przekrojów jak i inne właściwości figur znajdziesz po litreką [i]
Wo – wskaźnik wytrzymałości przekroju (na skręcanie) w biegunie o
e_max – odległość włókna najbardziej oddalonego od środka zginania lub skręcania
Dla przekroju spoiny pachwinowej tensor naprężeń zastępczych przyjmje postać naprężeń tnących i jest wypadkową tensorów wynikających z obciążeń dla konkretnego punktu spoiny
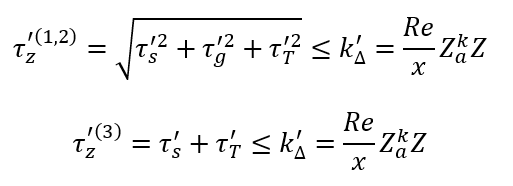
Przekrój II-II

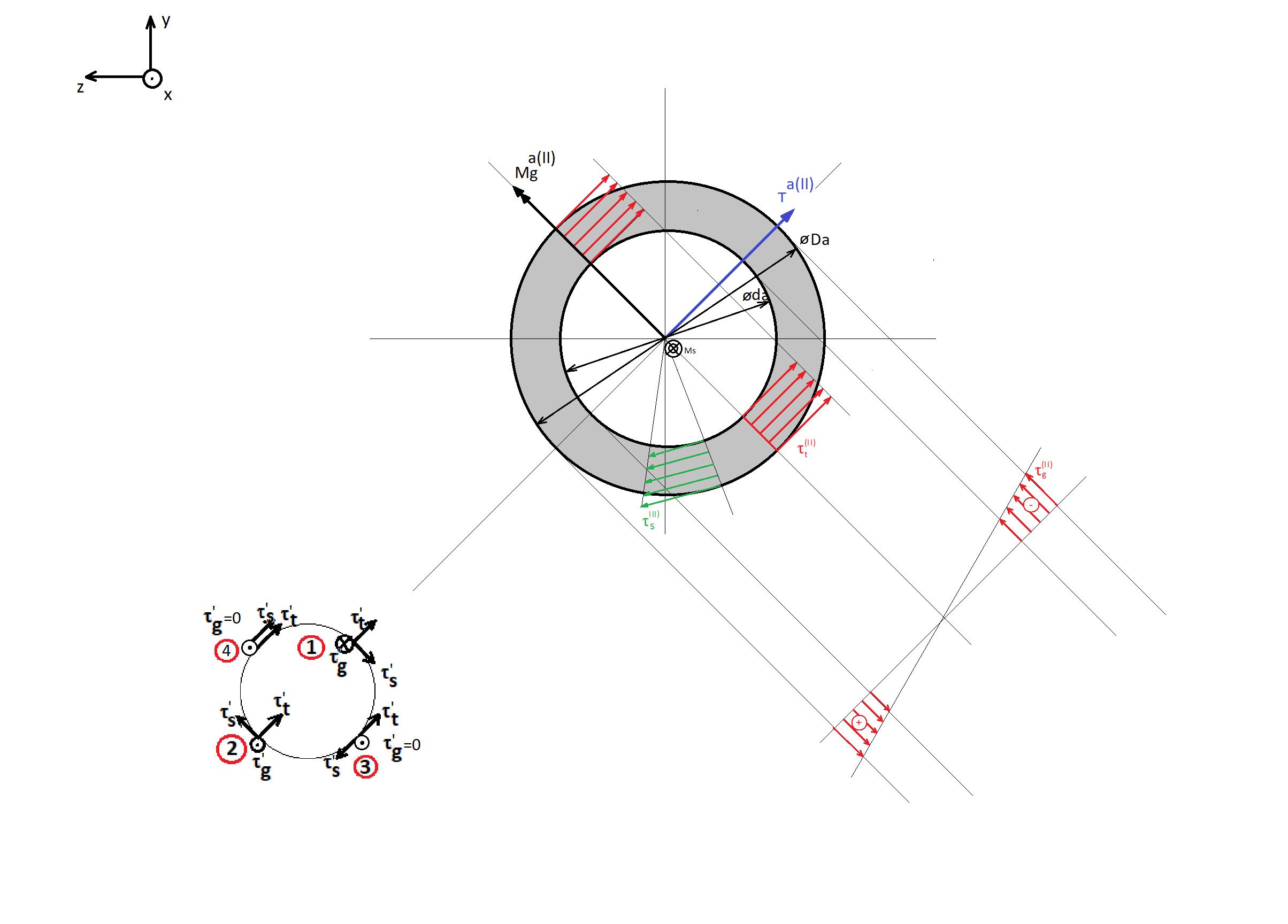
Obliczamy tensory naprężeń
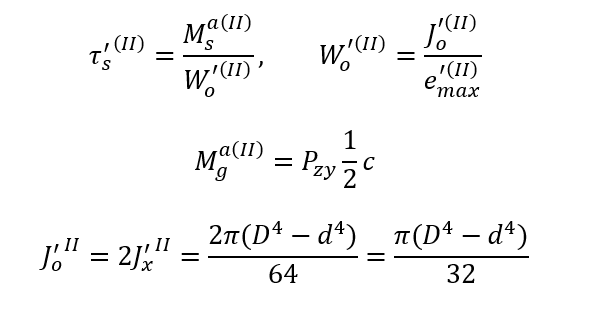
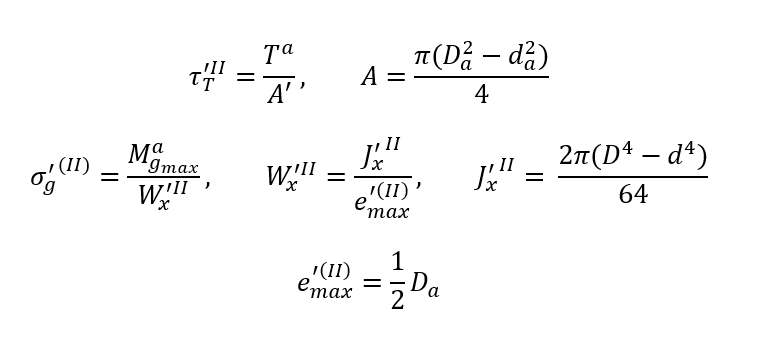

gdzie
Jx – moment bezwładności względem wprowadzonej osi obojętnej zginania x
Jo = 2Jx – biegunowy moment bezwładności – suma momentów osiowych względem
prostopadłych osi przechodzących przez ten biegun.
Wx – wskaźnik wytrzymałości przekroju (na zginanie) w osi x. Wskaźniki wytrzymałości przekrojów jak i inne właściwości figur znajdziesz po litreką [i]
Wo – wskaźnik wytrzymałości przekroju (na skręcanie) w biegunie o
e_max – odległość włókna najbardziej oddalonego od środka zginania lub skręcania
Przekrój III-III
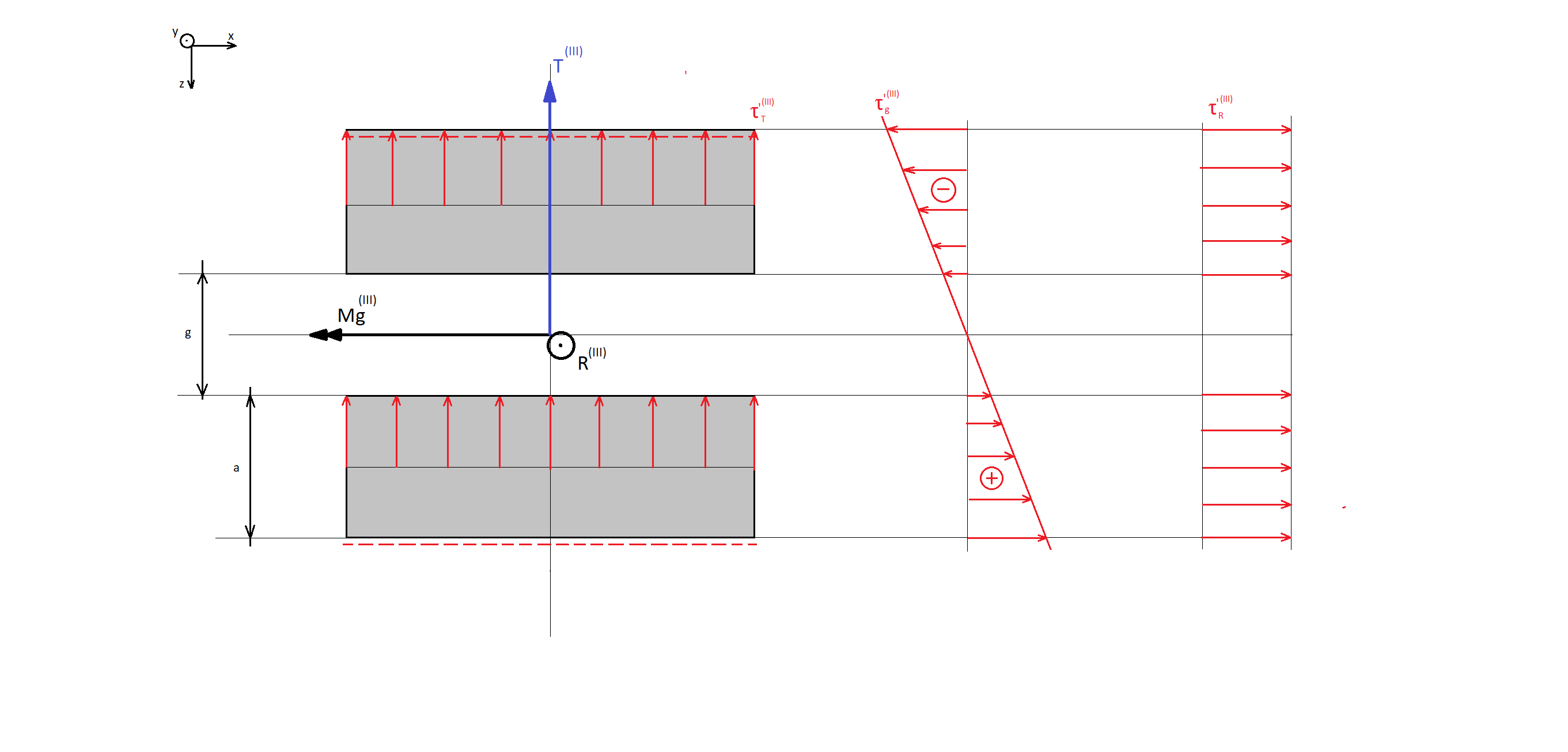
Obliczamy tensory naprężeń
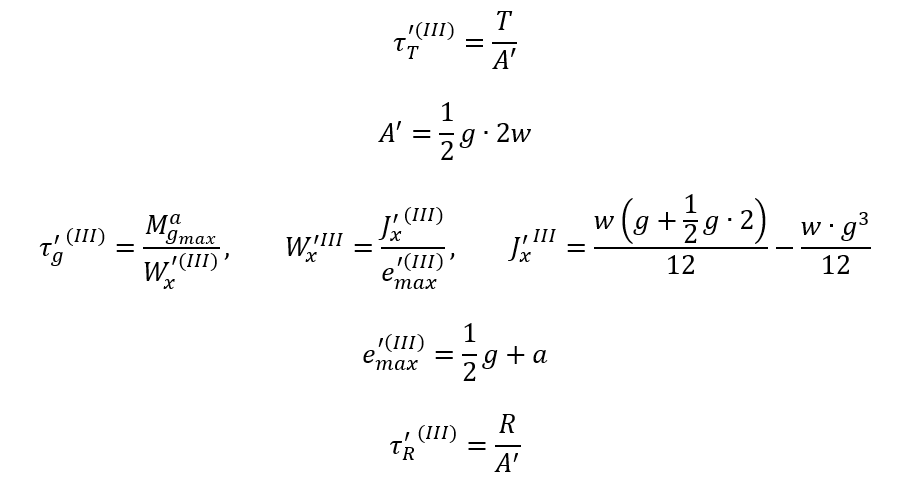
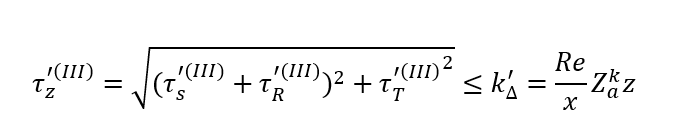
Przekrój IV-IV
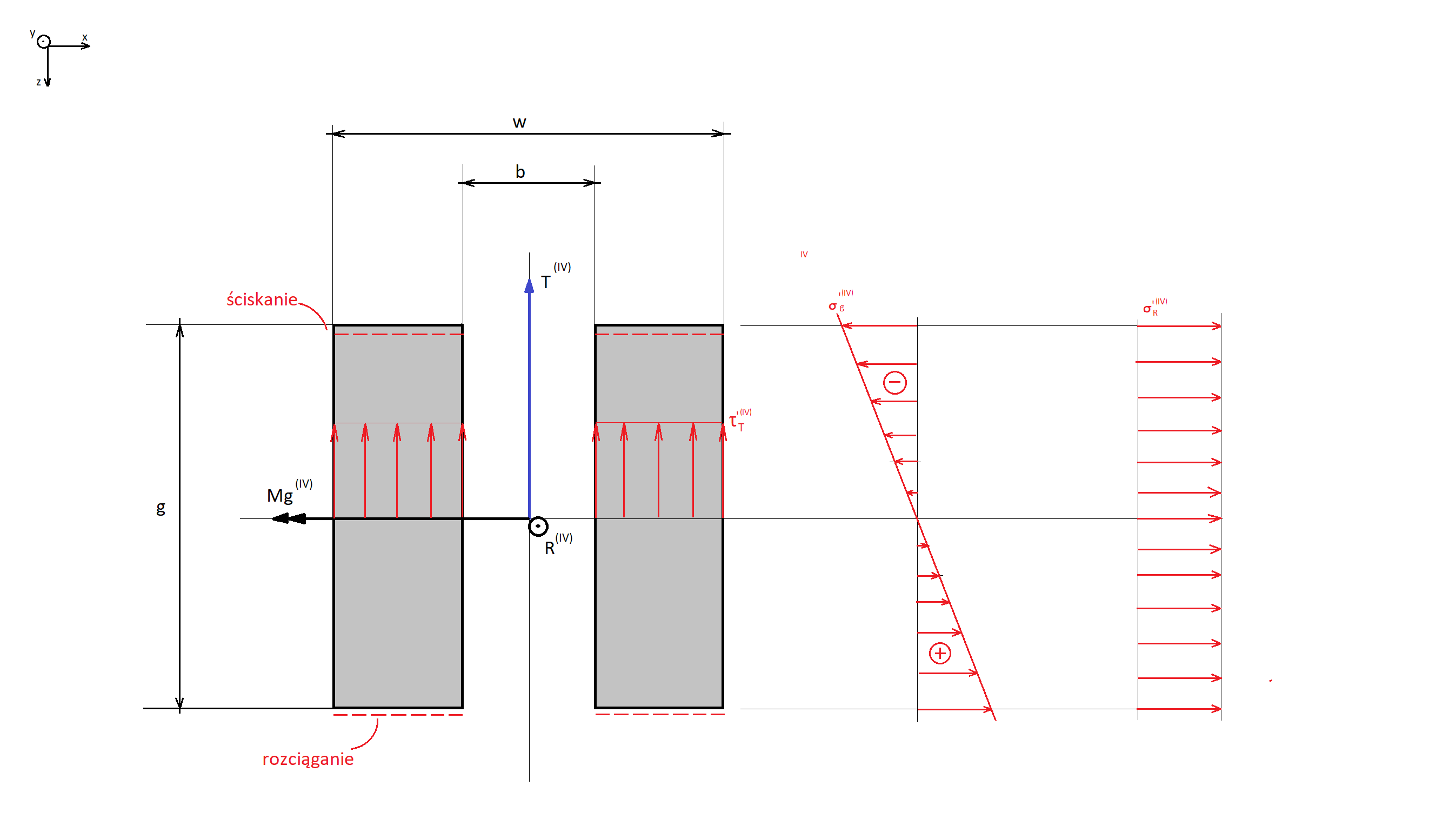
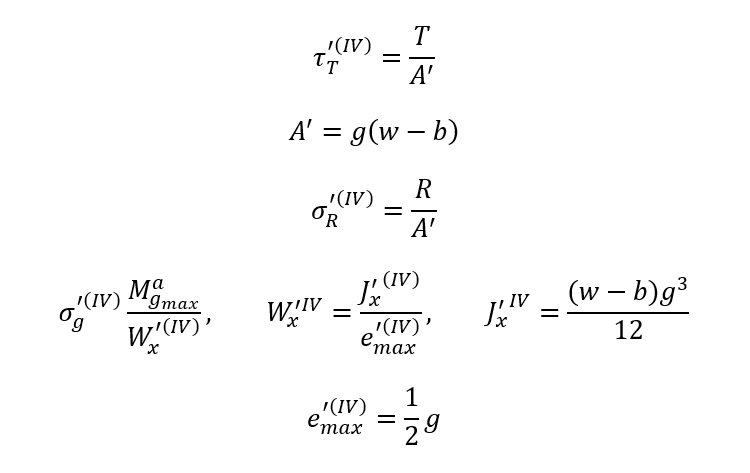
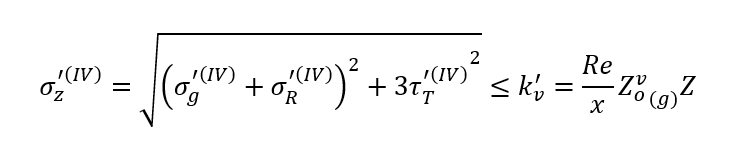
Są to gotowe wzory na obliczanie konstrukcji spawanych. Miejscem niebezpiecznym spoiny jest punkt w którym naprężenia zastępcze przekraczają dopuszczalne naprężenia na spoinie. Należy pamiętać, że obliczenia stanowią jedynie formę poglądową i nie są one gwarancją wytrzymałości. Proces spawania jest często procesem nieprzewidywalnym, wiele zależy od spawacza, materiałow oraz urządzeń spawalniczych.
Aby obliczenia były bardziej przewidywalne należy
- Dbać o stan narzędzi oraz przechowywać je w odpowiedni sposób – np. nie dopuścić do zawilgocenia elektrody otulinowej.
- Czyścić spoinę przed spawaniem i odtłuścić w miarę możliwości – np, alkoholem.
- Osuszyć miejsce spawania.
- Dbać o odpowiednią jakość gazów osłonowych.
- W przypadku spawania TIG dodatkowo zadbać o prawidłowy kształt końcówki elektrody wolframowej.
- Spawać gotowe detale na parametrach opracowanych na elementach próbnych.
- Wiedzieć jaki materiał spawamy np. poprzez dbanie o certyfikaty materiałowe, zapewniają one, że materiał ma konkretny skład chemiczny co w przypadku spawania jest kluczowe.
Obliczenia Spoiny Skręcanej i Zginanej
Treść : Wspornik traktowany jako metalowa konstrukcja spawana . Dla podanych danych i przypadków wyznaczyć wartość siły P, która może być przyłożona do dźwigni z uwagi na wytrzymałość złączy spawanych.
Rozważymy dwa przypadki obciążenia:
Pierwszy dla spoiny pachwinowej
Drugi dla spoiny czołowej
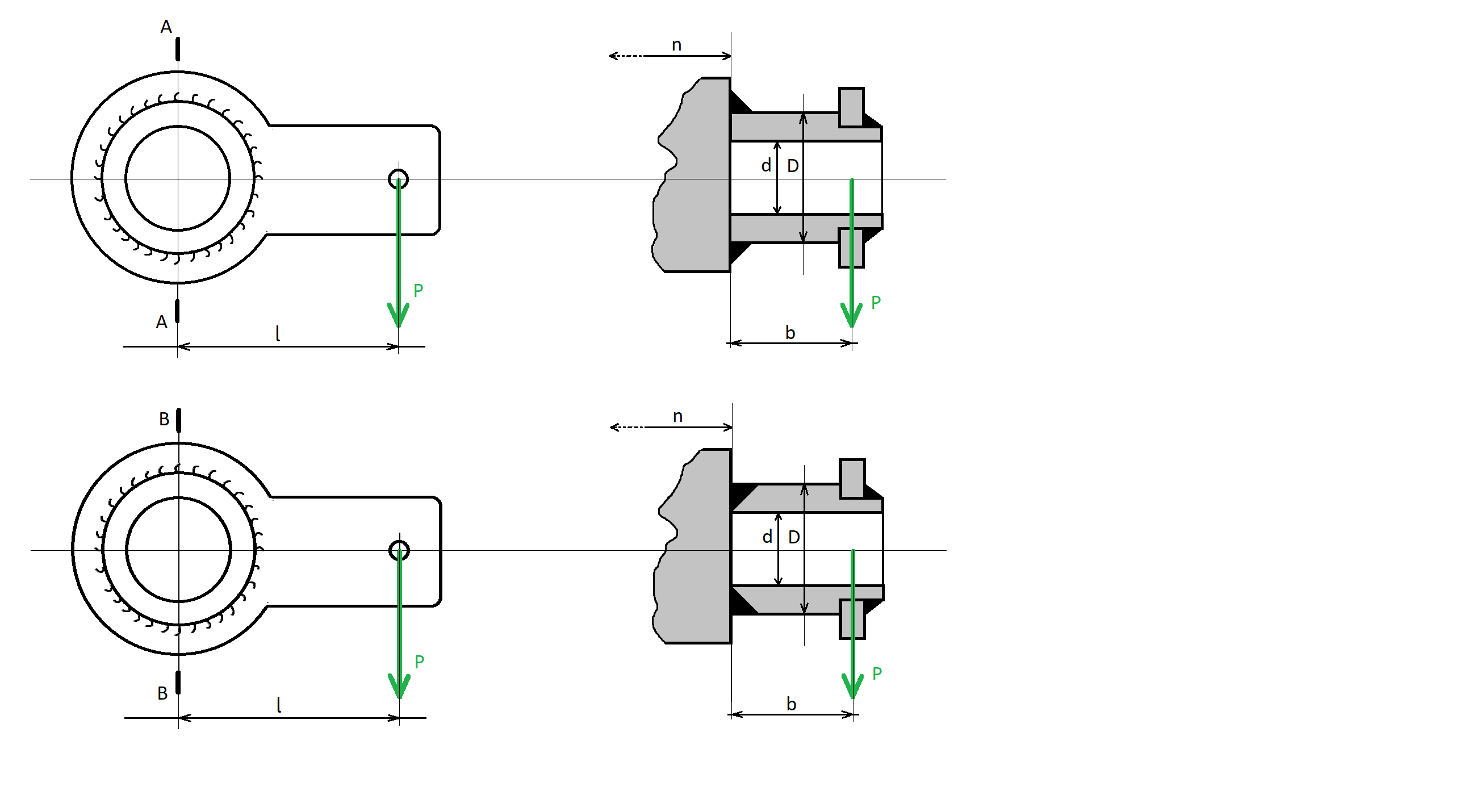
Dane:
D,d,b,L,Re,Rm,x,Z,Zovg,Zovr,Zost,Zo
Re-440MPa – granica plastyczności
Rm = 600MPa – granica wytrzymałości materiału na rozciąganie
μ = 0 – wzpółczynnik tarcia
X=2,5 – współczynnik bezpieczeństwa
Na początku należy wprowadzić uproszczony model belkowy układu
Obliczenia sił i momentów działających na wspornik :
Długie ramie a i krótkie ramie b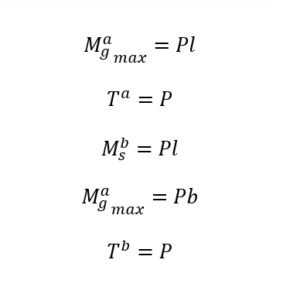 Następnym krokiem jest naniesienie rozkładów sił i momentów na uproszczonym modelu belkowym.
Następnym krokiem jest naniesienie rozkładów sił i momentów na uproszczonym modelu belkowym.
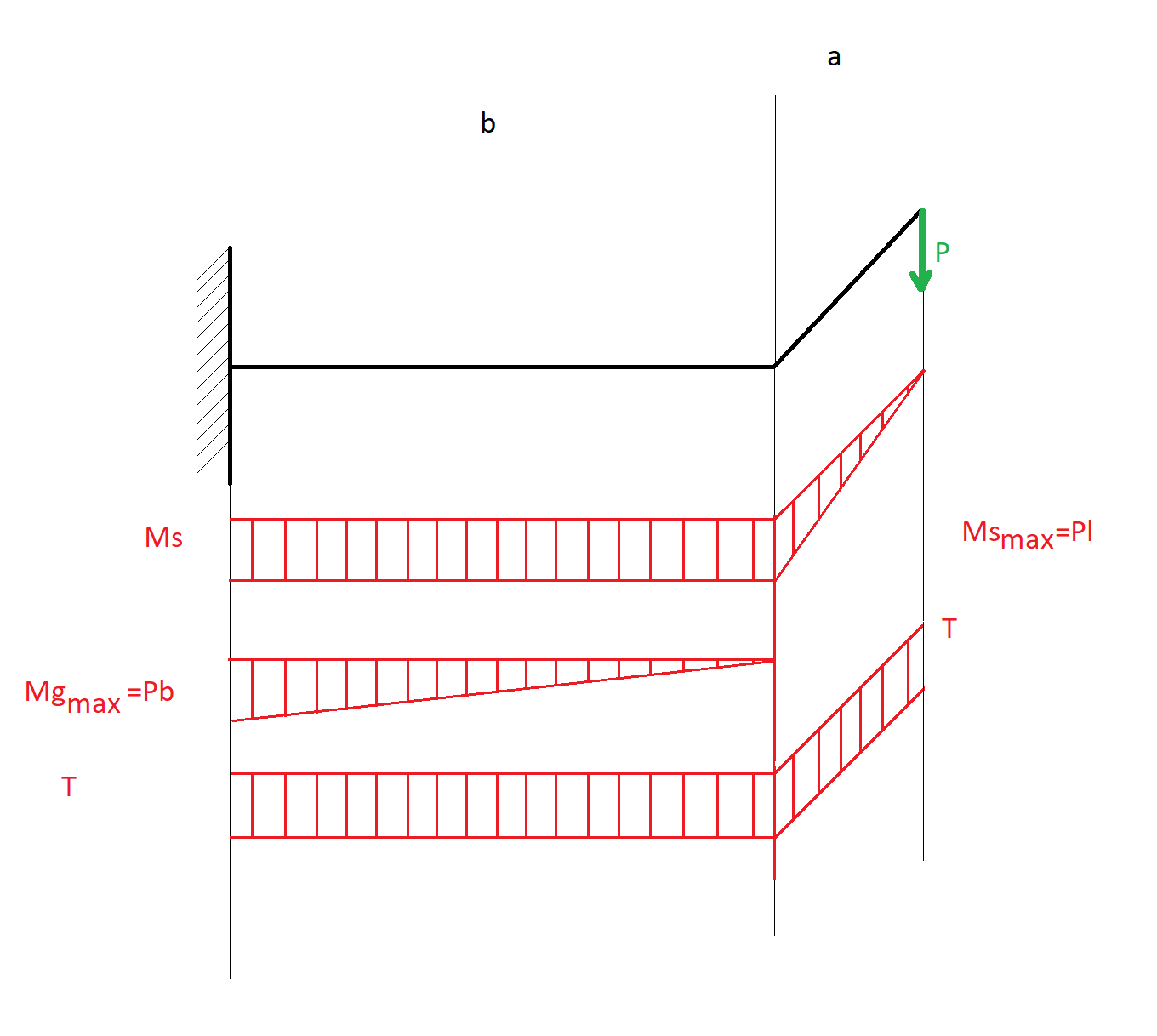
Na podstawie rozkładów sił, oraz geometrii należy wyznaczyć przekroje – takie przekroje wspornika w których może coś się stać – np. Spiętrzenie naprężeń, największe naprężenia itp.
Obliczanie Przekroju niebezpiecznego spoiny
Przekrój spoiny dla pierwszego przypadku – spoiny pachwinowej
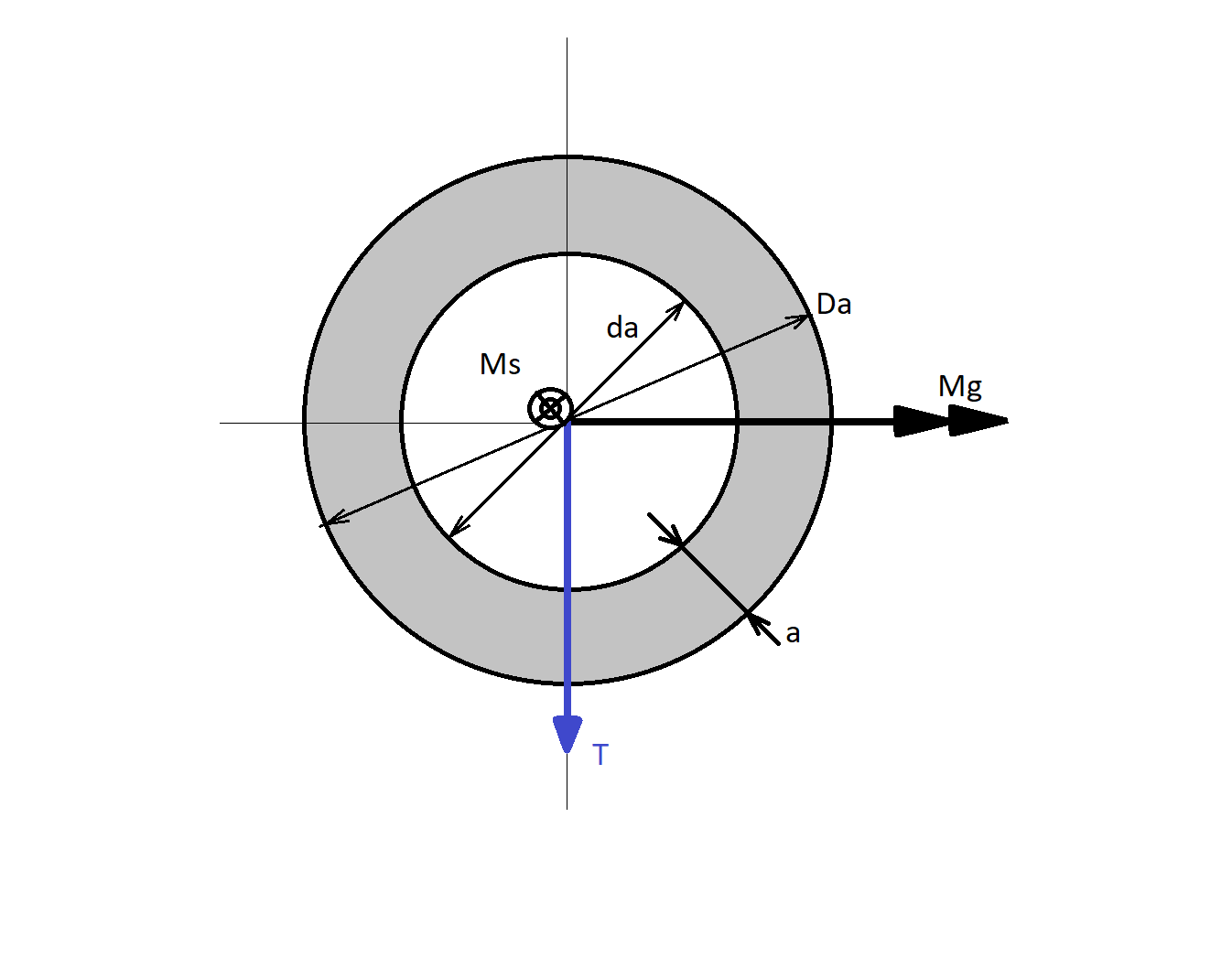
Dla spoiny pachwinowej obowiązuje zależność grubości spoiny do grubości ściany
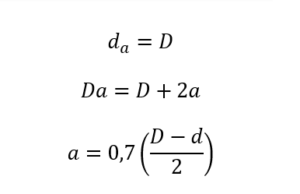
Warto zanotować, że w przypadku w którym rura zmienia się w walec obowiązuje zależność: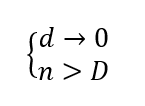
to traktujemy tę spoinę jako jednostronną pachwinową, na ścianie o boku D/2 zawiniętej wokół osi.
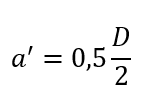 Natomiast gdy rura zmienia się w walec i
Natomiast gdy rura zmienia się w walec i
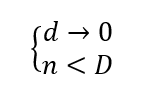
to
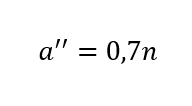
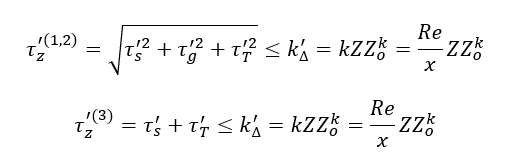
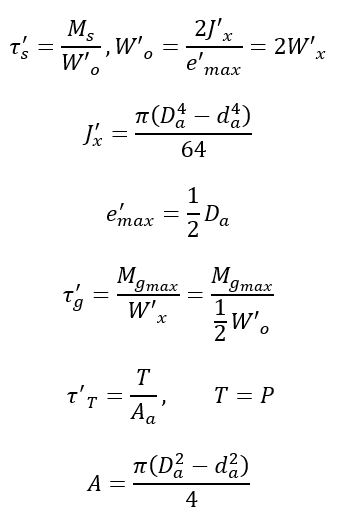
gdzie
Z_o^k- współczynnik dla spoiny pachwinowej
Jx – moment bezwładności względem wprowadzonej osi obojętnej zginania x
Jo = 2Jx biegunowy moment bezwładności – suma momentów osiowych względem
prostopadłych osi przechodzących przez ten biegun.
Wx – wskaźnik wytrzymałości przekroju (na zginanie) w osi x [i]
Wo – wskaźnik wytrzymałości przekroju (na skręcanie) w biegunie o
e_max – odległość włókna najbardziej oddalonego od środka zginania lub skręcania
Obliczenia maksymalnych dopuszczalnych sił dla punktów niebezpiecznych spoiny pachwinowej zgodnie z hipoezą wytężeniową Hubera z uwzględnieniem wzpółczynników dla spoiny pachwinowej, żadna z nich nie może przekroczyć wartości po prawej stronie równania
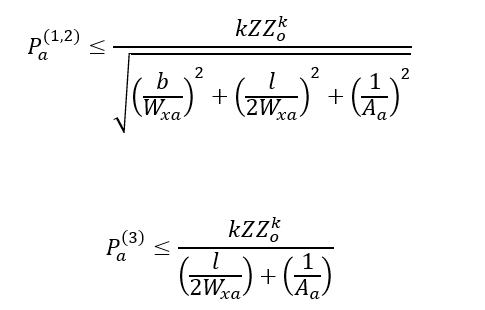
Obliczanie Przekroju niebezpiecznego spoiny
Przekrój spoiny dla drugiego przypadku – spoiny czołowej
gdzie
Jx – moment bezwładności względem wprowadzonej osi obojętnej zginania x
Jo = 2Jx – biegunowy moment bezwładności – suma momentów osiowych względem
prostopadłych osi przechodzących przez ten biegun.
Wx – wskaźnik wytrzymałości przekroju (na zginanie) w osi x [i]
Wo – wskaźnik wytrzymałości przekroju (na skręcanie) w biegunie o
e_max – odległość włókna najbardziej oddalonego od środka zginania lub skręcania
Następnie obliczamy, tensory naprężeń i naprężenia zastępcze
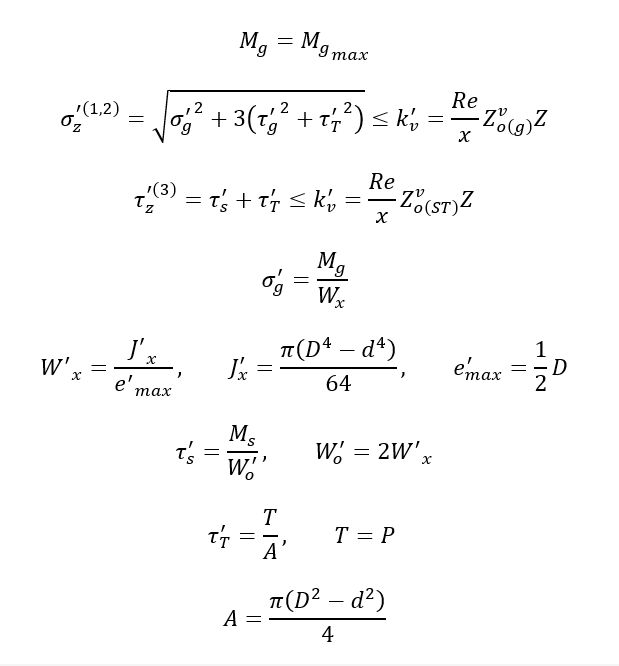
Obliczenia maksymalnych dopuszczalnych sił dla punktów niebezpiecznych spoiny czołowej zgodnie z hipoezą wytężeniową Hubera z uwzględnieniem wzpółczynników dla spoiny czołowej, żadna z nich nie może przekroczyć wartości po prawej stronie równania