Drgania wału
Drgania (oscylacje) – procesy, w trakcie których pewne wielkości fizyczne na przemian rosną i maleją w czasie. Każdy element posiada sztywność, która przy wychyleniu (dodaniu energii do układu) generuje siłę reakcyjną, dla której czas reakcji osiąga pewną specyficzną wartość. Układ wychylony o pewnej konkretnej sztywności i tłumieniu będzie oscylował wokół punktu równowagi tak długo jak tłumienie nie zaabsorbuje całkowicie energii wydanej na wychylenie. Częstotliwość z jaką element/układ drży pokrywa się z czasem reakcji siły reakcyjnej dla zadanej sztywności i nazywany jest częstością drgań własnych.
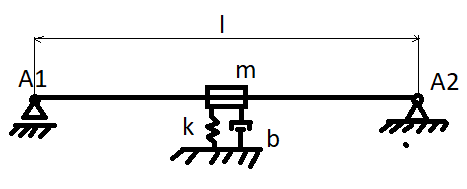
Jeśli częstość drgań własnych pokrywa się z częstością drgań wymuszonych lub jest jego wielokrotnością to dochodzi do zjawiska zwanego rezonansem, którego efektem jest wzrost amplitudy drgań.
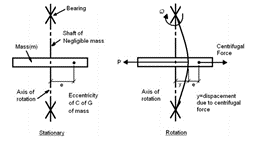
W przypadku wałów, jako elementów obrotowych parametrem wyjściowym będzie siła odśrodkowa działająca na wał
Sile tej przeciwdziała siła oporu sprężystości wału – reakcja którą możemy obliczyć ze strzałki ugięcia – dla wału dwupodporowego o sile skupionej w środku długości wału.
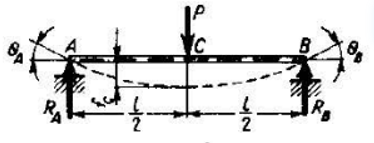
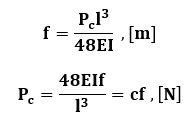
Porównując równanie na Pc z równaniem na PB:
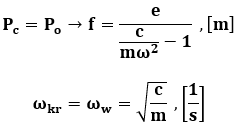
Gdzie:
ωkr -prędkość kątowa (prędkość krytyczna), przy której ugięcie rośnie nieskończenie
ωw – prędkość kątowa (częstość drgań własnych) dla drgań własnych.
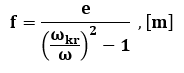
Prędkość obrotowa krytyczna:
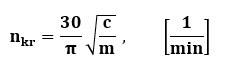
Jeśli częstość wymuszenia ω (w przypadku siły obciążającej stałej dla wału obracającego się – to prędkość kątowa obrotów) i częstość drgań własnych ωw są sobie równe to występuje zjawisko rezonansu. Co prowadzi do niekontrolowanego wzrostu amplitudy i złamania wału.
Do określenia ηkr wystarczy znać:
G – siłę obciążającą wału ciężarem = mg
fg – strzałkę ugięcia występującą na wale przy obciążeniu G
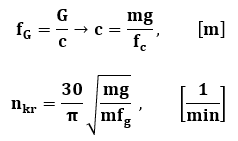
Gdzie :
g – przyśpieszenie grawitacyjne
Z zasady d’Alemberta :
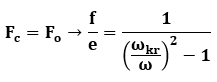
Fc – siła sprężystości wału
Fo – siła odśrodkowa wału
e -ekscentryczność środka ciężkości
f – dynamiczna strzałka ugięcia
wkr – prędkość kątowa krytyczna wału
w – prędkość kątowa wału
c -sztywność wału
m – masa skupiona
Nietłumione drgania giętne wału – rezonans
Trzeba uważać żeby nie przejść w rezonans ponieważ energia układu rośnie wtedy do nieskończoności – w praktyce aż do fizycznej granicy właściwości materiałowych.
W praktyce w wyniku tłumienia drgań –poprzez lożyska, histerezę materiału, opory powietrza itp. – ugięcie dynamiczne wału f nie osiąga wartości nieskończonej. Ponadto wystęuje efekt samo centrowania się wału giętkiego.
Zjawisko samocentrowania -przekroczenie prędkości obrotowej krytycznej dla ω→∞ to f→ev, wtedy – wypadkowa mimośrodowość dąży do 0.
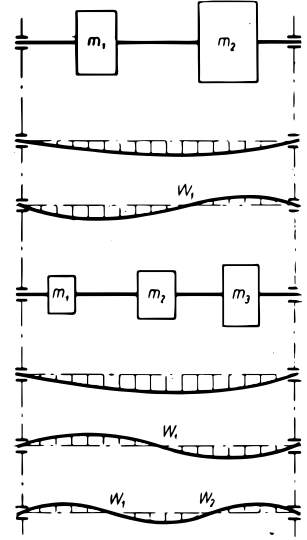
W przypadku układu o większej liczbie mas:
Istnieją konkretne częstotliwości rezonansowe dla każdej z mas (każdego układu):
Pierwsza częstość ω′ – odpowiada drganiom głównym, pierwszego rzędu.
Kolejne częstości ω″,ω″′częstościom wyższych rzędów.
Najgroźniejsze są drgania pierwszego rzędu – można obliczyć metodą Kulla
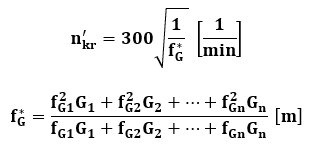
fGn – statyczne ugięcie wału pod ciężarem Gn , gdy wał obciążony każdym z ciężarów osobno.
W przypadku prędkości ponad-krytycznych należy jedynie szybko przejść przez prędkość rezonansową przy zwiększaniu prędkości.
Określić można niebezpieczny zakres prędkości w okolicy prędkości obrotowej krytyczniej. Mieści się on od 0,85ηkr do 1,25ηkr
Sposoby unikania rezonansu:
- Konstrukcja sztywnych wałów o wysokiej częstości drgań własnych im większa sztywność, tym większa prędkość krytyczna.
Drgania skrętne wału – długie wały które mają umieszczone ciężkie masy na sobie, nie mają problemu z częstością drgań skrętnych.
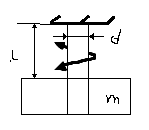
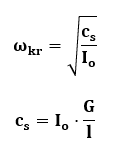
Gdzie:
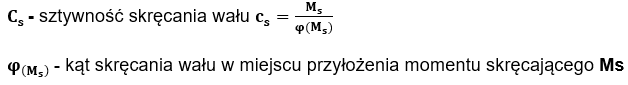
| Cs – sztwyność skręcania wału |
φ(ms) – kąt skręcenia wału w miejscu przyłożenia momentu skręcającego Ms
I0 – biegunowy moment bezwładności przekroju wału
G – moduł sztywności poprzecznej Kirchoffa
l – długość wału
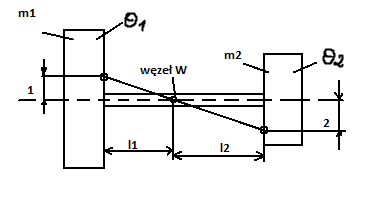
Dla wałów o „n” stopniach średnicach d1, d2, … , dn i długościach l1, l2, … , ln poszczególnych czopów
Schemat układu z dwoma masami, drgający skrętnie
Kąt skręcenia całej długości l:
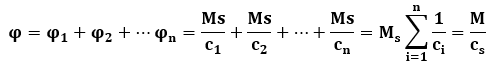
Sztywność zastępcza:
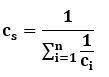
Długość zastępcza przy założonej jego średnicy dz:
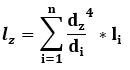
W przypadku wystąpienia sprzęgła sprzęgło można zastąpić odcinkiem wału o długości umownej Ls – długość sprzęgła i średnicy dz – średnica zastępcza wału odpowiadająca sztywności sprzęgła
Zastępcza długość sprzęgła:
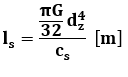
gdzie:
dz – dowolna średnica zastępcza
Przyjmujemy pełny okrągły wał o średnicy zastępczej równej średnicą sąsiednich czopó o długości l1z i l2z.
Całkowita długość wału zastępczego:
lz = l1z + l2z + ls
W takim wypadku obliczanie czętsości drgańwłasnych polega na obliczeniu częstości drgań wału o dowolnej średnicy dz i długości zastępczej lz.
