Hamulce klockowe
Hamulce klockowe – dzielimy je na jedno- lub dwuklockowe. Moment tarcia na bębnie hamulcowym ma zwrot przeciwny do zwrotu momentu obrotowego. W celu zahamowania bębna MT musi pokonać moment obrotowy i bezwładności hamowanego układu.
MT = (1,75 ÷ 2,5)Mo
Większe MT przyjmujemy, gdy jest duża prędkość obrotowa układu hamowanego oraz gdy żądamy, aby czas hamowania był krótszy.
Wartość nacisku siły klocka na bęben wynosi:
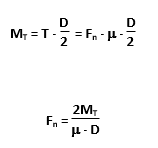
Siłę Fn będziemy traktować jako siłę skupioną zastępującą obciążenie ciągłe wynikające z nacisku klocka na bęben.
Obliczanie hamulców jednoklockowych, polega na wyznaczeniu siły F, którą należy przyłożyć do dźwigni hamulca, aby zahamować bęben, na ustaleniu wymiarów szczęki hamulcowej z warunku na naciski powierzchniowe, oraz sprawdzenia hamulca na rozgrzewanie.
Na elementy cierne hamulców stosujemy te same elementy co na sprzęgła cierne.
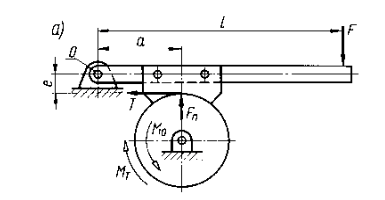
Rys 4.2
W hamulcu jak na rys 4.2 dźwignia hamulcowa jest zamocowana przegubowo w punkcie 0, a klocek jest połączony sztywno z dźwignią za pomocą dwóch sworzni. Na dźwignię działa siła Fn, siła F potrzebna do zahamowania bębna oraz siła tarcia T między klockiem a bębnem.
Dla dźwigni zwrot siły tarcia T jest zgodny z kierunkiem Mo, a dla bębna przeciwny.
Siły tworzą dowolny płaski układ – możemy więc wyznaczyć wartość siły F z warunku równowagi:
F ⋅ l – Fn ⋅ a + T ⋅ e = 0 [I]
Podstawiając do wzoru [I] wartość T otrzymamy:
T = Fn ⋅ μ
F ⋅ l – Fn ( a – e ⋅ μ) = 0 [II]
Wprowadzając do wzoru [II] wartość Fn otrzymujemy:
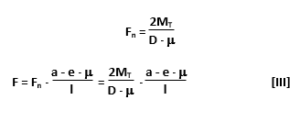
Zakładam przeciwny kierunek ruchu obrotowego bębna niż na rysunku.
Tak samo jak wyżej wyznaczamy F
![]()
Z porównania wzoru [III] i [IV], wynika, że hamulec ten nie nadaje się do pracy przy zmianie kierunku ruchu obrotowego, ponieważ należałoby regulować wartość siły F.
Jeżeli kierunek ruchu obrotowego bębna ma być zmienny, można stosować konstrukcje jak na
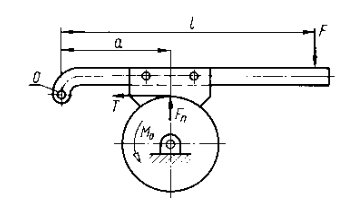
Rys 4.3
Wygięcie dźwigni w ten sposób, aby jej punkt obrotu 0 leżał na linii działania siły tarcia T powoduje, że ramię tej siły e = 0 i wobec tego e ⋅ μ = 0.
Wartość siły F koniecznej do zahamowania bębna wynosi wówczas:
![]()
Nie zależy ona w tym przypadku od kierunku ruchu obrotowego.
Taki sam efekt uzyskamy mocując klocek jak na rys.4.4
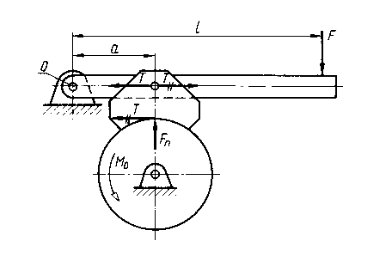
Rys.4.4
Siłę nacisku F1 traktujemy jako siłę działającą na sworzeń. Wprowadzamy w osi sworznia zerowy układ sił T, otrzymujemy siłę T działającą na sworzeń wzdłuż osi dźwigni oraz moment od pary sił T.
Moment ten dąży do obrócenia klocka i nie wpływa na obliczenia dźwigni. Przy tej konstrukcji wartość siły F wyznaczymy wg wzoru [V].
Obliczenia wymiarów klocka z warunku na naciski powierzchniowe:
![]()
gdzie:
t – długość klocka (mierzona po cięciwie łuku);
b – szerokość klocka;
ko – naciski dopuszczalne.
Zakładamy konstrukcyjnie „D” i „b”
Zalecenia D = 120 [mm] i b = 40 [mm] (160 – 50, 200 – 55, 250 – 80, 320 – 100, 400 – 125,
500 – 160, 630 – 200, 710 – 220, 800 – 250).
Szerokość bębna przyjmujemy o 10 mm > od b, natomiast t:
t = (0,52 ÷ 0,78)D
co odpowiada kątowi pokrycia ϕ = 60° ÷ 90°.
Hamulec sprawdzamy na rozgrzewanie wg wzoru:
(p ⋅ v)rzecz ≤ (p ⋅ v)dop [MN/m⋅s]
Hamulce jednoklockowe – średnica wału do 50 mm i przenoszenie niewielkich Mo.
Hamulce dwuklockowe – siły Fn równoważą się i umożliwiają hamowanie przy mniejszych Fn.
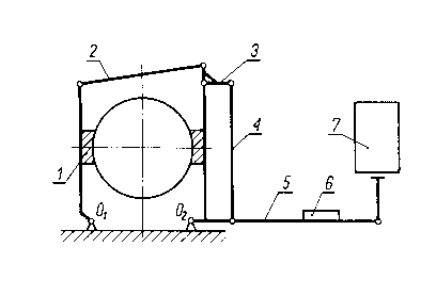
Rys. 4.5 Schemat hamulca dwuklockowego z luzownikiem: 1 – klocki hamulcowe, 2 ÷ 5 dźwignie, 6 – ciężar, 7 – luzownik
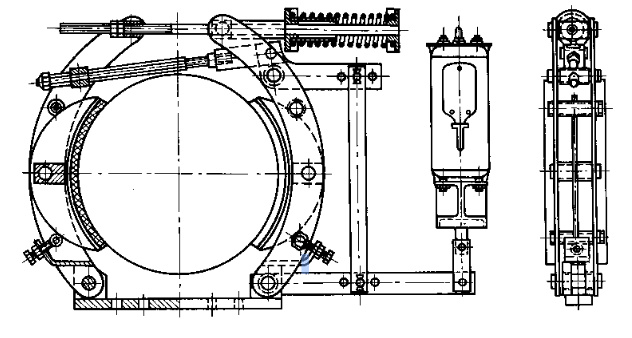
Rys.4.6 Hamulec dwuklockowy zwierany sprężyną i zwalniany luzownikiem elektromagnetycznym
