Hamulce cięgnowe
Hamulce cięgnowe – charakteryzują się większą skutecznością hamowania stosujemy, gdy występują duże Mo. Prosta konstrukcja, zwarta budowa.
Wada: zginanie wału pod wpływem naciągu cięgna.
Cięgna – cienka taśma stalowa wyłożona materiałem ciernym. Gdy niewielkie MH – nie ma okładziny.
Obliczanie tych hamulców polega na określeniu MT, niezbędnego do zahamowania bębna, obliczeniu wartości sił w cięgnie oraz obliczeniu siły F jaką należy przyłożyć do końca dźwigni.
Wartość MT ustalamy z założenia:
MT = (1,75 ÷ 2,5)M
Gdy będziemy mieli ustaloną średnicę bębna D ( z warunków konstrukcyjnych), możemy określić siłę tarcia T potrzebną do zahamowania bębna.
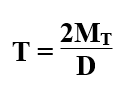
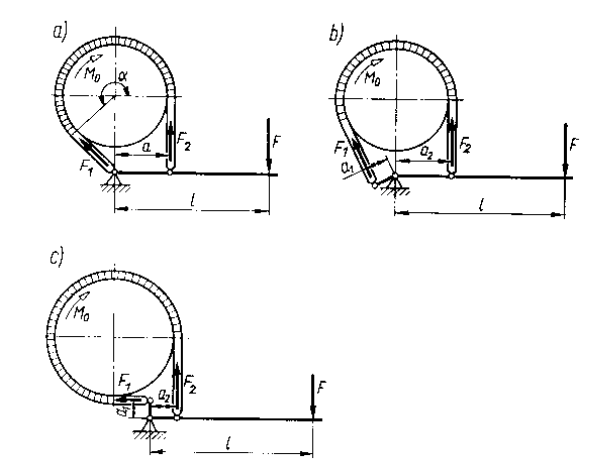
Rys.4.9 Hamulce cięgnowe: a) zwykły, b) różnicowy, c) sumowy
Hamulec zwykły – (rys 4.9a) cięgno współpracujące z bębnem na części jego obwodu (odpowiada to kątowi α).
W cięgnie wyróżniamy:
- część czynną – nabiegającą na bęben – działa w niej siła F1;
- część bierną – działa w niej siła F2.
siła F1 > F2
ponieważ część czynna cięgna obciążona jest dodatkowo siłą tarcia wywołaną momentem obrotowym T.
Z warunku równowagi:
T = F1 – F2 [I]
Stosunek sił F1 i F2 określa zależność (wzór Eulera). Określa on stosunek napięć w cięgnach:
| F1 = F2 ⋅ m gdzie | |
[II] |
Przyjmujemy α = 180° ÷ 270° (od π do 1,5π rad)
gdzie:
α – kąt opasania.
Na podstawie wzorów [I] i [II] wprowadzamy zależność między T a F1 i F2.
| oraz T = F2 ( m – 1) [III] |
Wartość siły F potrzebnej do zahamowania wyznaczamy z warunku równowagi sił działających na dźwignię. Wyznaczać je będziemy względem punktu 0, przyjmując kierunek ruchu obrotowego jak na rysunku (rys. 4.9 a, b, c)
W hamulcu zwykłym ( rys. 4.9 a) część czynna cięgna zamocowana w punkcie obrotu dźwigni – na dźwignię działają siły: F2 oraz F
Warunek równowagi przyjmie postać:
F ⋅ l – F2 ⋅ a = 0 [IV]
![]()
Zalecane przełożenie dźwigni l/a = 3 ÷ 6
Gdy zmienimy kierunek ruchu obrotowego, wówczas część czynna będzie pełnić funkcje części biernej i odwrotnie.
![]()
Hamulec różnicowy – (rys.4.9b)
Warunek równowagi dla hamulca różnicowego:
F ⋅ l + F1 ⋅ a1 – F2 ⋅ a2 = 0
stąd:
![]()
Po zmianie kierunku ruchu obrotowego:
![]()
Hamulec sumowy – (rys.4.9c)
Warunek równowagi dla hamulca sumowego (a1 = a2 = a)
F ⋅ l – F1 ⋅ a – F2 ⋅ a = 0
stąd:
![]()
Po zmianie kierunku ruchu obrotowego bębna (w stosunku do podanego na rysunku c) wówczas częścią czynną cięgna będzie dotychczasowa część bierna i odwrotnie.
![]()
Na podstawie przeprowadzonej analizy hamulców:
- Hamulec zwykły i różnicowy zastosujemy tam, gdzie jest stały kierunek ruchu obrotowego bębna i wału.
- W hamulcu różnicowym odpowiednio dobierając długości dźwigni a1 i a2 – regulujemy F (przy niewłaściwej długości tych dźwigni F = 0 lub F< 0 (samo zakleszczanie).
Aby uniknąć samo zakleszczenia spełniamy warunek:
![]()
- Hamulec sumowy (a1 = a2 = a) – siła obciążająca F jest jednakowa dla obydwu kierunków obrotu ale dość duża jej wartość przekreśla zastosowanie tego hamulca.
- Przy ruchu dwukierunkowym – hamulec dwuklockowy.
Hamulce dzielimy na:
- zaciskowe;
- luzowe.
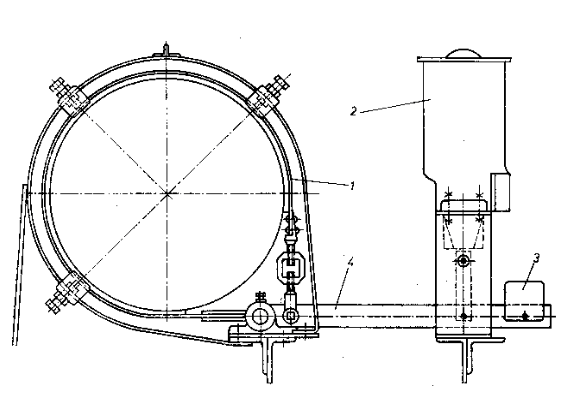
Rys.4.10 Konstrukcja hamulca taśmowego zwykłego: 1 – taśma, 2 – zwalniak, 3 – obciążnik, 4 – dźwignia

Rys. 4.11 Hamulec zwrotny: 1 – śruba, 2 – wał, 3 – bęben, 4 – zapadki, 5 – sworzeń zapadki, 6 – koło zapadkowe, 7 – wieniec koła hamulcowego, 8 – dźwignia hamulca, 9 – taśma hamulca
