Obliczanie przekładni z pasami klinowymi.
Zależności z obliczeń dla przekładni pasowych z pasem płaskim obowiązują dla przekładni z pasem klinowym. Drobne różnice sprowadzają się do:
- kąt opasania α na małym kole przyjmuje się już powyżej 70° (dla pasów płaskich – powyżej 120°), co wynika m.in. z mniejszych odległości osi;
- odległość osi przyjmuje się orientacyjnie w granicach 0,5(dp1 + dp2) + 50 mm < a ≤ 2 (dp1 + dp2);
- dla pasów klinowych przyjmuje się współczynnik napędu φgr = 0,5 ÷ 0,7 oraz dopuszczalną częstotliwość zginania Gmax = 20 ÷ 40s – 1;
- zamiast średnic kół gładkich wykorzystujemy we wzorach średnice skuteczne (dp) .
Metodyka obliczeń wg PN – 67/M – 85203.
Powinniśmy mieć założenia konstrukcyjne: P1, n1, i, (dodatkowo może być a).
- Na podstawie złożeń konstrukcyjnych przyjmujemy średnice skuteczne dp1, dp2.
- W zależności od i przyjmujemy k1 i obliczamy średnice równoważne.
De = dp1 · k1
gdzie:
k1 = 1 dla i = 1
k1 = 1,15 dla i = 0,55 ÷ 1,8
dp1 – średnica koła mniejszego.
3. Obliczamy prędkość pasa
![]() 4. Sprawdzamy warunek odległości osi a.
4. Sprawdzamy warunek odległości osi a.
0,5(dp1 + dp2) + 50 < a < 2(dp1 + dp2)
5. Obliczamy kąt opasania koła mniejszego α.
![]()
6. Obliczamy kąt rozwarcia cięgien g.
γ = π – α π = 180°
7. Obliczamy długość pasa
![]()
8. Dobieramy L znormalizowane wg trybu pasa.
9. Obliczamy liczbę pasów
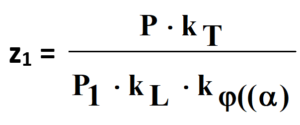
gdzie:
P – moc przenoszona przez przekładnię;
P1 – moc przenoszona przez jeden pas klinowy;
kT – współczynnik trwałości pasa zależny od h (pracy na dobę kT = (1 ÷ 1,8);
kL – współczynnik trwałości pasa zależny od typu i długości kL = (0,72 ÷ 1,2);
kφ(α) – współczynnik kąta opasania kφ = (0,7 ÷ 1);
φ – kąt opasania;
10. Sprawdzamy trwałość pasa.
![]()
Gmax = 40 s – 1
11. Przyjmujemy:
dla dwóch kół z = 2
dla dwóch kół i rolki z = 3
