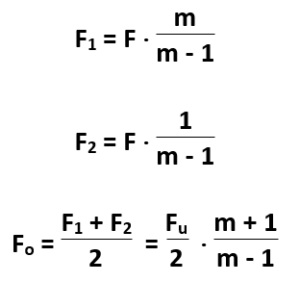Obliczanie przekładni z pasem płaskim
Jako podstawowe przyjmujemy założenia, którymi są:
- moc P1
- prędkość obrotowa n1 (koło napędzające);
- wartość przełożenia i;
- materiał pasa;
- dodatkowo a (przeważnie a ≈ (1,5 ÷ 2)(D1 + D2)
Wg tych wartości wyznaczamy wymiary przekładni (średnice kół i ich rozstawienie) oraz wymiary pasa.
Tok obliczeń dla przekładni o i > 1
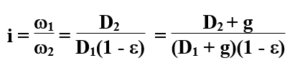
gdzie:
g – grubość pasa;
ε – poślizg sprężysty (e = 0,01 ¸ 0,02).
Wymiary średnic obliczeniowych ustalamy na osi obojętnej pasa (D+g). W obliczeniach wstępnych g można pominąć ze względu na mały stosunek g/D.
Średnicę obu kół możemy przyjąć wg założeń konstrukcyjnych (nie obliczamy), ewentualnie z zależności:
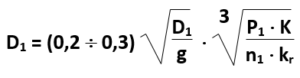
gdzie:
D1 – orientacyjna wartość średnicy małego koła

Charakterystyczne współczynniki dola pasów:
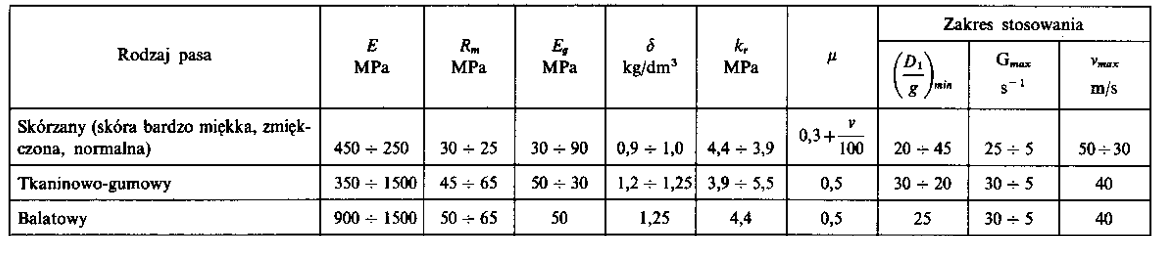
P1 – przenoszona moc [kW];
K – współczynnik przeciążenia (dla przekładni pasowych – tablica 13.2 Cz.m);
kr – naprężenia dopuszczalne dla materiału pasa.
Wyznaczone średnice zaokrąglamy do znormalizowanych Prędkość pasa – 30 ÷60 m/s ( ograniczona własnościami wytrzymałościowymi – vmax – tablice)
Po założeniu D1 i D2 sprawdzamy vpasa
W przekładniach o dużych mocach i szybkobieżnych, dążymy do vmax – D1 wyznaczamy z wzoru:
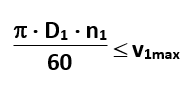
Podstawowe parametry geometryczne przekładni:
α – kąt opasania na małym kole;
γ – kąt rozwarcia cięgien;
a – rozstawienie osi kół (1,5¸2);
L – długość pasa napiętego (mierzona na osi obojętnej);
D1,D2 – średnice obliczeniowe kół.
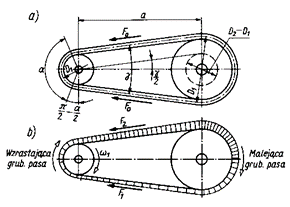
Rys.2.11 Przekładnia pasowa: a) w stanie spoczynku, b) w ruchu
Kąt opasania wyznacza się następująco:
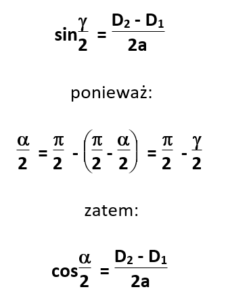
Długość pasa L oblicza się jako sumę długości odcinków prostoliniowych i długości odcinków opasujących koła:
![]()
Dla pasów płaskich zaleca się: α = 120° , tj. 2/3 π [rad] (na małym kole).
Cięgno – w spoczynku lub ruch jałowy – powinno być napięte z siłą Fo (napięcie wstępne) wówczas naprężenie w pasie wyniesie:
![]()
gdzie:
S – pole przekroju pasa;
Fo – napięcie wstępne.
Aby uzyskać żądane napięcie wstępne (w ramach odkształceń sprężystych pasa), przed założeniem pas powinien być krótszy o wielkość ΔL.Wartość tę wyznaczę zgodnie z prawem Hookea wg wzoru:
![]()
gdzie:
E – moduł sprężystości pasa;
Lo – długość swobodna pasa (pierwotna).
Powyższy wzór przekształcamy tak, aby otrzymać wzór na Lo (przekładnia o „a” stałym).
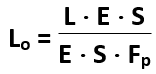
Uruchamiamy przekładnię – wskutek tarcia między pasem a powierzchnią kół część czynna cięgna (nachodząca na koło czynne) jest dodatkowo rozciągana i napięcie jej rośnie od Fo do F1. W części biernej pasa napięcie maleje do F2.
Porównujemy wartość napięć w cięgnie czynnym i biernym w czasie spoczynku i podczas ruchu:
Wyznaczamy:
Fo = 0,5 (F1 + F2)
Napięcie użyteczne:
Fu = F1 – F2 = F
Napięcie użyteczne stanowi siłę obwodową F wg której określamy Mo przenoszony przez pas.
Przenoszoną moc wyznaczamy z zależności:
P1 = F · v1 = Fu · v1 [P1] = N · m/s = W
Moc obliczeniowa:
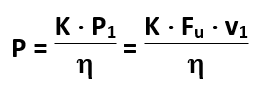
gdzie:
η – sprawność przekładni pasowej, (0,94 ¸ 0,98) – przeciętne warunki pracy.
Podstawą do obliczeń napędów cięgnowych jest wzór Eulera, określający stosunek napięć w cięgnie czynnym i biernym.
![]()
gdzie:
e – podstawa logarytmu naturalnego (e » 2,7182);
α – kąt opasania dla mniejszego koła [rad];
μ– współczynnik tarcia między pasem a kołem (wg tablicy 13.1 Cz.M.).
Dla uproszczenia wprowadza się wartość:
![]()
Wówczas
F1 = F2 · m
Z podanej zależności wynika, że mając wartość siły obwodowej (F = Fu), jaką powinna przenieść dana przekładnia pasowa, oraz wartość m (dla danego a i m) obliczamy wartość poszczególnych napięć: