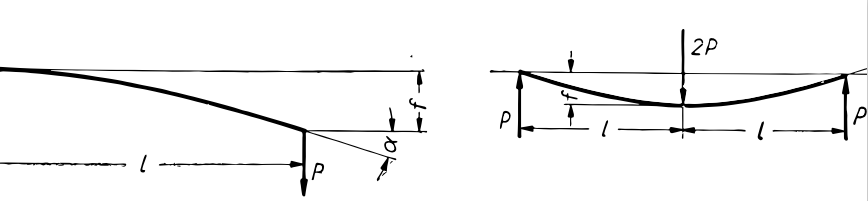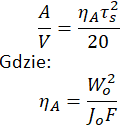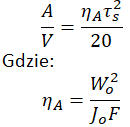Projektowanie sprężyn pojedynczych
Sprężyny o pręcie skręcanym
Warunki Wytrzymałościowe:
| – współczynnik stałości obciążeń |
k_sj – dopuszczalne naprężenia skręcające jednostronie zmienne
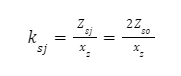
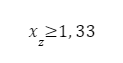
przykładowe orientacyjne wartości parametrów dla Prętów skręcanych
![]()
Parametry wytrzymałościowe dla druta d_o=5mm ze stali węglowej lub stopowej ciągnionego i zwijanego na zimno
| Rodzaj drutu | Z_so | k_s | k_sj | k_sj/k_s |
| Drut ciągniony | 150-170 | 500-550 | 220,5-250,5 | 0,40-0,45 |
| Drut szlifowany | 200-250 | 550-600 | 300-370,5 | 0,55-0,65 |
| Drut szlifowany oraz hartowany i niskoodpuszczany | 280-320 | 600-750 | 420-480 | 0,65-0,75 |
przykładowe orientacyjne wartości parametrów dla Prętów skręcanych
![]()
Parametry wytrzymałościowe dla druta d_o=5mm ze stali węglowej lub stopowej ciągnionego i zwijanego na zimno
| Rodzaj drutu | Z_so | k_s | k_sj | k_sj/k_s |
| Drut ciągniony | 150-170 | 500-550 | 220,5-250,5 | 0,40-0,45 |
| Drut szlifowany | 200-250 | 550-600 | 300-370,5 | 0,55-0,65 |
| Drut szlifowany oraz hartowany i niskoodpuszczany | 280-320 | 600-750 | 420-480 | 0,65-0,75 |
Parametry wytrzymałościowe dla grubego druta zwijanego na gorąco, hartowanego i nisko odpuszczanego
| Rodzaj drutu | Z_so | k_s | k_sj | k_sj/k_s |
| Walcowany | 40-60 | 300-405 | 60-90 | 0,2-0,3 |
| Szlifowany | 100-160 | 400-550 | 150-240 | 0,35-0,45 |
Parametry wytrzymałościowe dla pręta ze stali – sprężynowej chromowo-wanadowej 50HF PN-74/H-84032 hartowany i niskoodpuszczony
| Rodzaj Pręta | Z_so | k_s | k_sj | k_sj/k_s | ||
| Ø20 | Ø40 | Ø60 | ||||
| Pręt szlifowany | 200 | 170 | 100 | 500-650 | 150-300 | 0,3-0,45 |
| Pręt zgniatany | 300 | 280 | 200 | 300-405 | 300-450 | 0,5-0,6 |
Dla obciążeń statycznych sprężyny
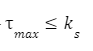
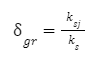 |
– graniczna wartość współczynnika stałości obciążenia, przy której uzyskuje się jednakowe bezpieczeństwo w warunkach statycznych i dynamicznych |
| Jeśli |
– decyduje wytrzymałość statyczna |
| Jeśli |
– decyduje wytrzymałość zmęczeniowa |
k_s – dopuszczalne naprężenia skręcające dla obciażeń stałych
k_sj – dopuszczalne naprężenia skręcające jednostronie zmienne
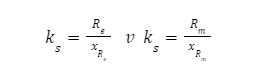
Rm – granica wytrzymałości na rozciąganie – stosowane dla stali twardych, pękających
Wytrzymałość z uwzględnieniem spółczynnika kształtu i wymiaru przekroju:
g_k – współczynnik kształtu
g_w – współczynnik przekroju, zazwyczaj pozyskiwane z gotowych tablic, wzór na g_w
g_f – współczynnik wytrzymałości przekroju pręta
Tablica wartości współczynników dla sprężyn o pręcie skręcanym o przekroju okrągłym
| D/d | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 14 | 16 |
| g_k | 0,645 | 0,725 | 0,775 | 0,813 | 0,833 | 0,855 | 0,870 | 0,884 | 0,905 | 0,918 | 0,925 |
| g_d | 0,292 | 0,268 | 0,248 | 0,232 | 0,2175 | 0,206 | 0,196 | 0,187 | 0,173 | 0,161 | 0,152 |
| g_f | 0,1075 | 0,0905 | 0,0775 | 0,0677 | 0,0595 | 0,0534 | 0,0489 | 0,0446 | 0,0381 | 0,033 | 0,0194 |
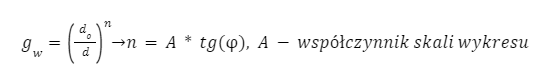
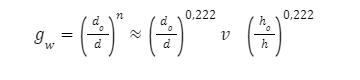
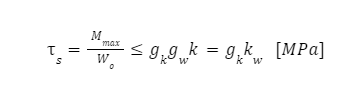
| – dopuszczalne naprężenie dla pręta prostego uwzględniające wymiary przekroju i warunki obciążenia |
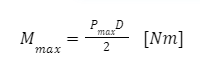
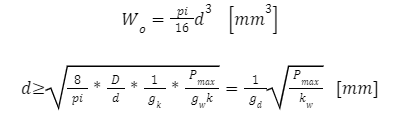
| – współczynnik wytrzymałościowy średnicy pręta |
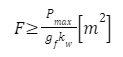
| – współczynnik wytrzymałości przekroju pręta |
Zestawienie wzrów dla sprężyn o pręcie skręcanym
Dla drążka skrętnego
| Naprężenie skręcające | Kąt skręcenia lub strzałka ugięcia | Sztywność sprężyny | Praca odkształcenia | Zdolność akumulowania energii |
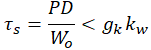 |
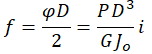 |
|
Dla sprężyny śrubowej
| Naprężenie skręcające | Kąt skręcenia lub strzałka ugięcia | Sztywność sprężyny | Praca odkształcenia | Zdolność akumulowania energii |
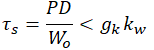 |
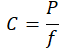 |
 |
|
Dla pręta o przekroju okrągłym
| Średnica, przekrój pręta | Ugięcie zwoju f/i | Wskaźnik wytrzymałości przekroju w osi przekroju | Moment bezwładności przekroju w osi | Współczynnik równomierności rozmieszczenia naprężeń |
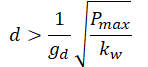 |
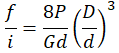 |
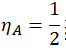 |
Dla pręta o przekroju prostokątnym,
| Średnica, przekrój pręta | Ugięcie zwoju f/i | Wskaźnik wytrzymałości przekroju w osi przekroju | Moment bezwładności przekroju w osi | Współczynnik równomierności rozmieszczenia naprężeń |
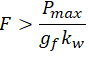 |
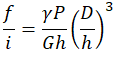 |
Wartości współczynników do obliczania spręzyn śrubowych o prostokątnym pręcie skręcanym
| b/h | 1,0 | 1,5 | 2 | 3 | 4 | 5 |
| η_2 | 0,208 | 0,231 | 0,246 | 0,267 | 0,282 | 0,29 |
| η_3 | 0,140 | 0,196 | 0,229 | 0,263 | 0,281 | 0,29 |
| 0,308 | 0,272 | 0,264 | 0,272 | 0,282 | 0,29 | |
| γ | 5,60 | 2,67 | 1,70 | 1 | 0,7 | 0,54 |
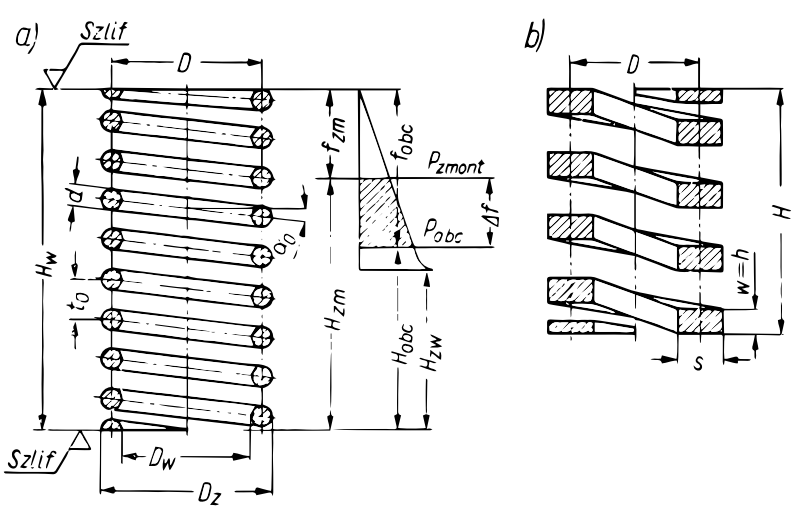
Sprężyny śrubowe walcowe, naciskowe z drutu okrągłego:
-duża podatność
-duża zdolność do akumulowania energii
-brak uchwytów
-dobre wykorzystanie materiału i przestrzeni
-centryczne przeniesienie siły
Końce śruby zaciśnięte i zeszlifowane co najmniej ¾ obwodu. Dla dużych sprężyn (o dużym d ) końcówki są rozkuwane
Nawet przy największym obciążeniu Qmax powinien zostać zachowany luz
Dla nieobciążonej sprężyny kąt wzniosu linii śrubowej powinien wynosić 8*
Jednym z parametrów obliczeniowych sprężyn jest strzałka ugięcia jednego zwoju:
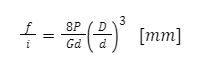
| – całkowita liczba zwojów sprężyny, wartość 1,5…2 wynika z zagięcia i zeszlifowania pierwszego i ostatniego zwoju sprężyny w celu zapewnienia odpowiedniego podparcia | |
| – wysokość spreżyny zwartej (ściśniętej do punktu zwarcia zwojów) |
| – wysokość sprężyny obciążonej |
Gdzie
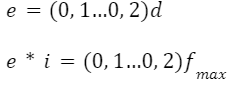
e – najmniejszy luz między zwojami pod obciążeniem P_max
dodatkowo
| – wysokość sprężyny zamontowanej pod obciążeniem P_min | |
| |
– wysokość sprężyny w stanie wolnym – nieobciążonej |
Dla sprężyn stalowych
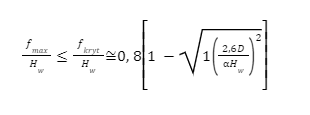
α – współczynnik zależny od sposobu osadzenia i obciążenia sprężyny
α≅1 – dla sprężyn bez prowadzenia
α≅0,5 – dla sprężyn dokładnie prowadzonych
α≅2 – dla sprężyn dodatkowo zginanych
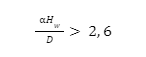

Warunek wytrzymałościowy
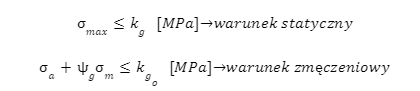

Z wykresu Haigha
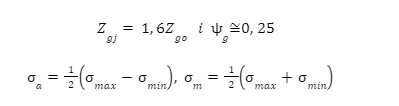
δ-współczynnik stałości obciążenia pręta zginanego

| – graniczna wartość współczynnika stałości obciążenia, przy której uzyskuje się jednakowe bezpieczeństwo w warunkach statycznych i dynamicznych | |
| Jeśli |
– decyduje wytrzymałość statyczna |
| Jeśli |
– decyduje wytrzymałość zmęczeniowa |
k_g – dopuszczalne naprężenia gnące dla obciażeń stałych
k_gj – dopuszczalne naprężenia gnące jednostronie zmienne
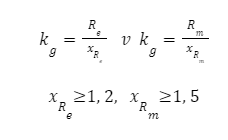
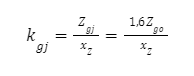

Przykładowe orientacyjne wartości parametrów dla Prętów zginanych
![]()
Pręt ze stali stopowej hartowanej i nisko odpuszczonej z Re~ 1400MPa
| Rodzaj Pręta | Z_go | k_g | k_gj | k_gj/k_g |
| Pręt walcowany | 130-210 | 550-750 | 160-250 | 0,25-0,35 |
| Pręt kulkowany | 310-340 | 650-900 | 370-400 | 0,45-0,55 |
| Pręt szlifowany | 410-460 | 700-950 | 500-550 | 0,55-0,70 |
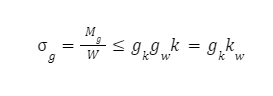
gk – współczynnik kształtu pręta, jedynie uwzględniany w przypadku dużej krzywizny pręta (duży stosunek wymiaru przekroju do promienia krzywizny w płaszczyźnie działania momentu gnącego
Wzory obliczeniowe do obliczeń spręzyn o pręcie zginanym
Według rodzaju pręta
Dla pręta o stałym przekroju
| Naprężenie gnące | Strzałka ugięcia | Kąt wychylenia końca pręta | Współczynnik równomierności rozmieszczenia naprężeń |
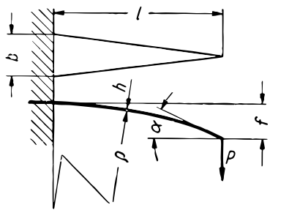
Dla pręta trapezowego
| Naprężenie gnące | Strzałka ugięcia | Kąt wychylenia końca pręta | Współczynnik równomierności rozmieszczenia naprężeń |
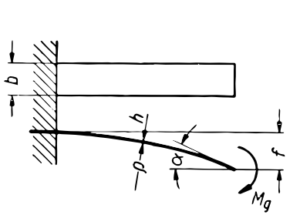
Dla pręta obciążonego momentem gnącym
| Naprężenie gnące | Strzałka ugięcia | Kąt wychylenia końca pręta | Współczynnik równomierności rozmieszczenia naprężeń |
Według przekroju pręta:
Dla pręta prostokątnego
| Wskaźnik wytrzymałości przekroju | Moment bezwładności przekroju | Obiętość czynna pręta sprężyny | Współczynnik równomierności rozmieszczenia naprężeń |
Dla pręta okrągłego
| Wskaźnik wytrzymałości przekroju | Moment bezwładności przekroju | Obiętość czynna pręta sprężyny | Współczynnik równomierności rozmieszczenia naprężeń |
Współczynniki kształtu dla pręta zginanego sprężyny
| D/d lub Ds. | 3 | 4 | 5 | 6 | 8 | 10 |
| Przekrój okrągły | 1,33 | 1,23 | 1,17 | 1,13 | 1,08 | 1,05 |
| Prostokątny | 1,29 | 1,20 | 1,15 | 1,12 | 1,08 | 1,06 |
Współczynniki dla pręta trapezowego
| b_o/L | 1,0 | 0,8 | 0,6 | 0,4 | 0,2 | 0 |
| y1 | 1,0 | 1,05 | 1,12 | 1,20 | 1,31 | 1,5 |
| y2 | 1,0 | 1,07 | 1,17 | 1,30 | 1,49 | 2,0 |
| ηA | 0,111 | 0,130 | 0,155 | 0,19 | 0,242 | 0,333 |
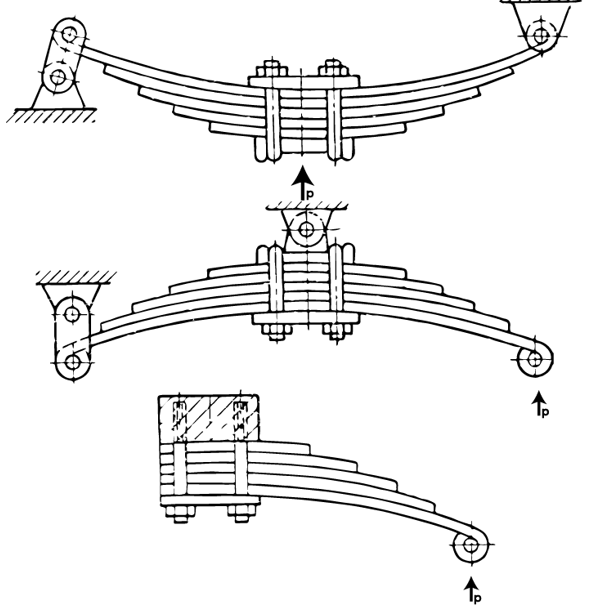
Sprężyny płaskie pojedyncze